ゼロから作るDeep Learning ❹ ―強化学習編 を読んで実装した

オライリーから出ている、「ゼロから作るDeep Learning ❹ ―強化学習編」を読んで実装した。

実装はこのリポジトリにある。 https://github.com/kamiteku557/deep-learning-from-scrach-4github.com

読んだ感想

内容としては、強化学習とは何か・その目的から始まり、ベルマン（最適）方程式の導出、DP・モンテカルロ法、TD法、DQNへと続き、方策勾配法とActor-Criticまでをカバーしている。
強化学習に触れたのはこの本が初めてだったが、かなりわかりやすかったと思う。
ただその一方で、内容はかなり浅瀬を泳いでいる風だったので、これを読んでも「強化学習を実務で使う」だったり「最新論文を読んだら理解できる」という段階にはまだまだ遠いな...という感じ。
（特に、強化学習に必須そうな、並列処理の話とかはなかった。他の実装本だと書いているんだろうか？）

強化学習については、論文を読むなり他の本を読むなりでもう少し勉強したいな。

以下の本は良さそう。

www.amazon.co.jp

www.amazon.co.jp

www.amazon.co.jp

www.amazon.co.jp

実装の際に参考にしたもの・役立ったもの

• OpenAI Gym を Jupyter Notebook で動かすために、gym-notebook-wrapperを使用した。
  • インストールも使用方法も非常に楽でかなり助かった。

gitlab.com

• pytorch周りのTypeHintはtorchtypingを使って書けるらしい。
  • 使い方は 【PyTorch】テンソルのデータ型や形状をアノテーションするtorchtypingを使ってみた - yiskw note がわかりやすかった。

github.com

• 変数の値を確認するときに、printの代わりにicecream というライブラリを使うと、変数と値が同時に確認できて便利だった。
  • icecreamの使い方は IceCream使い方まとめ - Qiita など。

github.com

Advanced Database Systems(2020)のOptimizer Implementation(Part1~3)を視聴したときのメモ

Advanced Database Systemsという講義のOptimizer Implementation(Part 1~3)を視聴したときのメモ。殆どPart1の内容。

基礎事項

クエリ最適化とは

• クエリに対して、コストが最も小さく、正しい実行計画を探すこと
• コストは実行時間やデータサイズ、CPU/IO/ネットワーク使用量など様々な視点がある
• DBMSの構成要素の中でもかなり難しい部分(最適な計画を探すのはNP-Complete)
• そのため、コストの推定や探索空間を減らすためのヒューリスティクスを使う

logical plan と physical plan
ざっくり、logical planは「何をするのか」を論理演算子で定義したもので、
physical planは「どうやってするのか」をアクセスパスのレベルで定義したもの。 　 　
オプティマイザはlogical planを最適で等価なpysical planへの対応を生成する。　　
(この対応は1:1とは限らない)

オプティマイザを設計するときに考えること

講義では以下の軸が紹介されていた。

最適化の粒度

• Single Query 　
  • 探索空間が狭い。他クエリの結果を再利用することは一般にない。
• Multiple Query
  • 探索空間が広い。クエリ間で結果をシェアするので、類似するクエリが多い場合に効率的。　

最適化のタイミング

• Static Optimization
  • 実行前に最適な計画を選ぶ。 Prepared Statementを使用して実行を償却できる？
• Dynamic Optimization
  • 実行時に最適な計画を選ぶ。複数の実行に対して再最適化される。　　　
• Adaptive Optimization
  • 静的アルゴリズムを用いたコンパイル。推定コストがしきい値を超える場合、再変更/再最適化される。 　　

Prepared Statementとは、以下のように一部の値が変数に置き換わったクエリのこと。

PREPRARE MyQuery AS    
    SELECT *  
    FROM table  
    WHERE value > ?  
    
EXECUTE myQuery(10) # SELECT * FROM table WHERE value > 10  

Prepared Statements

• 最後の計画を再使用
  • 前実行時に生成された計画を再利用　　
• 再最適化
  • クエリが実行されるたびにオプティマイザを実行する。(注: 出発点として既存の計画を再利用するのは難しいらしい。) 　
• 複数の計画　　
  • パラメタ(引数)の値によって別々の実行計画を生成する
• 平均の計画
  • パラメタの平均値を選択し、それをすべての呼び出しに使用する。

プランの安全性

• ヒントの提供
  • DBAがオプティマイザにヒントを提供できるようにする
• オプティマイザのバージョンを固定
  • オプティマイザのバージョン番号を設定し、クエリを1つずつ新しいオプティマイザに移行する。(?)　　
• 計画の後方互換性
  • 古いバージョンからのクエリを保存し、新しいDBMSに提供する

検索の終了条件

• Wall-clock
  • オプティマイザが一定時間実行された後に停止　　
• Costの閾値　　
  • コストが閾値より小さいプランが見つかったら停止
• Exhaustion
  • ターゲットプランの列挙がなくなったら停止。通常、グループ毎に実施される。(?)

#### 最適計画の探索手法
講義では以下の手法が紹介されていた。
リストの下に行くほど新しく複雑な手法になっていく。

• ヒューリスティクス
  • 静的なルールに基づき、論理演算を physical plan に変換する。
  • ex: INGRES, 昔のOracle
  • Pros : 実装が容易で、単純なクエリなら十分に良い結果を素早く得られる
  • Cons: マジックナンバーに頼る形になる。また、複雑なクエリにで良い結果を得るのは難しい
• ヒューリスティクス + Cost-based Join Order Search
  • ルールによる最適化の後、動的計画法によりjoinの順序を調整する。bottom-upの手法。
  • ex: System R, 多くのOSSであるDBMS
  • Pros : 通常、網羅的な検索を実行せずにいい感じの計画が得られる
  • Cons: コストを考える時、データの物理的な性質を考慮に入れる必要がある。また、ヒューリスティクスのConsを引き継ぐ。
• 乱択アルゴリズム
  • 探索範囲でランダムウォークを実施する。焼きなましとかも。
  • ex : Posgresの遺伝的アルゴリズム
  • Pros : 局所的な最適解を避けることができる。また、メモリのオーバーヘットは低い(履歴を保持しないならば)
  • Cons: なぜその実行計画が選ばれたのか解釈が難しく、再現性を担保する仕組みが必要。また、実行計画が正しいものであるかのルールが必要。
• Stratified Search : 層別検索
  • ２ステップに分けて実行する。
    1. logical -> logical ... logical planを変換ルールを使って書き換える。この時、その変換が許されるかを確認する。また、このステップでコストは考慮されない。
    2. logical -> physical ... コストに基づく探索を行い、logical planを physical plan に対応させる。
  • ex : Starburst
  • Pros : 実際、いい感じに機能する
  • Cons: 変換に優先順位を割り当てるのが難しく、ルールのメンテナンスのコストが大きい。
• Unified Search : 統合検索 (Volcano)
  • logical -> logicalとlogical -> physicalの概念を統合する。また、多くの変換が生成されるので、メモ化により冗長な作業を減らす。top-downの手法。
  • Pros : 宣言的なルールを使って変換を生成する。メモ化。
  • Cons: 全ての等価なクラスは完全に拡張され、最適化検索の前に全ての可能な論理演算子を生成する。一方、述語を変更するのは容易ではない。

WIP【備忘録】DBの論文を読む : 弱い分離と配布

そろそろデータベースに関するちゃんとした基礎知識をつけたいという思いがあるので、Readings in Database Systems, 5th Edition を読んでいこうと思う。
URL: http://www.redbook.io/index.html

この本は、DBに関する古典的な論文から、近年の特に重要な論文まで、章ごとに短い解説とともに紹介されている。

今回は Ch6 Weak Isolation and Distribution を読む。

紹介された論文

1. Generalized Isolation Level Definitions. ICDE, 2000.

   • あああ

2. Dynamo: Amazon's Highly Available Key-Value Store. SOSP, 2007.

   • いいい

3. CAP Twelve Years Later: How the "Rules" Have Changed. IEEE Computer, 45, 2 (2012).

   • ううう

解説を読んだ

この章では、以下のことを説明している。

• 実際のDBではトランザクション(以下, txn)の分離レベルとしてSerializableよりも「弱い分離レベル」を使用する場合が多いこと、そしてその理由
• 「弱い分離レベル」が実際に何をしているのか
• それらについての推論が難しい理由

著者は弱い分離が一般的である理由として、「(必要な？)調整が少ない」「パフォーマンスが高い」「可用性が高い」等を挙げた上で、以下のように述べている。

• 直列化不可能な分離は、並行性に関して利点があるため（従来のRDBMSと最近のNoSQLの新興企業の両方で）普及している
• しかし、直列化不可能な分離に関する多くの既存の定式化は、十分に規定されておらず、使用するのが困難
• 弱い分離の研究は、意味のあるセマンティクスを維持し、直列化可能性を犠牲にすることなくプログラム可能性を改善する方法を示している

「アプリケーション開発者の中には直列化できない分離レベルのもとで実行されている事に気が付かない人がいる」と言われて耳が痛かった...。

なんでこの章でNoSQLの論文が出てくるんだろう？と疑問だったけど、以下のような解説があった。

NoSQLは分散環境向けに最適化された一連の新しいデータストアとして登場したが、その重要な特徴として、NoSQLはフォールトトレランスに明確に焦点を当てて、より弱いモデルを介して操作の可用性を向上させることに焦点を当てていることが多い。

なるほど。

論文1について

Abstruct

• 現在のANSI規格では分離レベルが定義されているが、それは以下のような問題がある
  • 定義が曖昧
  • ロックに基づいており、「実装に依存しない」というANSISQLの目標を満たしていない
    • これにより、マルチバージョンを含む楽観的アルゴリズムによる分離レベルをカバーしていない
• この論文では以下の貢献をしている
  • 実装に依存しない方法で既存のANSI分離レベルを規定する
  • さらに、その方法は述語(WHERE)を正しく処理することができる
  • その定義では、コミットされたtxnと実行中のtxnに対して異なる分離保証を行うことができる
    • 本稿では、コミットされたトランザクションに対する保証のみを提示する
      　　　

要約とメモ

ロックに基づく分離レベルの復習

分離レベルはPhenomenaと呼ばれる良くない動作をどの程度禁止するかという観点で作られていた。
phonomenaとしては以下のP0~P4があった。記法の確認も一緒にして欲しい。

# wn[x]: n番目のtxnにおいてxに対して書き込みを行う
# wn[x in P]: n番目のtxnにおいて述語Pのxに対して書き込みを行う
# rn[x]: n番目のtxnにおいてxに対して読み出しを行う
# rn[P]: n番目のtxnにおいて述語Pのレコードの読み出しを行う
# cn   : n番目のtxnをcommit
# an   : n番目のtxnをabort


P0: w1[x] ... w2[x] ... (c1 or a1)
P1: w1[x] ... r2[x] ... (c1 or a1)
P2: r1[x] ... w2[x] ... (c1 or a1)
P3: r1[P] ... w2[y in P] ... (c1 or a1)

また、ロックに基づく分離レベルを以下のように表としてまとめることができる。

出典 [1]

用語: Long lock ... ロックをかけたtxnがcommitされるまで保持される Short lock ... ロックをかけるキッカケとなった読み取り/書き込み処理が完了した直後に解放される

因みに、ロックは特定の状況(例えば、2つのtxnが同時に同じオブジェクトを変更する)を防ぐことでtxnを直列化するため、このアプローチを予防的アプローチと呼ぶ。

しかし、この予防的アプローチは以下のような問題点がある。 - このアプローチは制限的すぎる。事実、楽観的なマルチバージョン実装を排除している。
- バージョンではなくオブジェクトの観点から記述されているため、マルチバージョンシステムには適用できない - phenomenaが単一オブジェクトの履歴で表現されている - 関心のある特性は、多くの場合複数オブジェクトの制約(ex x+y=10)

例を考える。 x+y=10という制約がある場合において、以下のようなtxnの履歴(history)を考える。

H1: r1(x, 5) w1(x, 1) r2(x, 1) r2(y, 5) c2 r1(y, 5) w1(y, 9) c1
H2: r2(x, 5) r1(x, 5) w1(x, 1) r1(y, 5) w1(y, 9) c1 r2(y, 9) c2

分離レベルはSERIALIZABLE 両方ともT2からは制約が満たされない状態である。(H1はP1に該当, H2はP2に該当)

TODO: 追記

道具の用意1

database model - DBはtxnによって読み書きができるオブジェクトで構成される
- オブジェクトは１つ以上のバージョンを持つ。txnはDBとオブジェクトに関してのみ影響し合う - txnがオブジェクトxを書き込んだとき、xの新しいバージョンが作成される。txn Tiはあるオブジェクトxiを複数回修正でき、xi:1, xi:2, ...と表記される。 - txnがcommitされた時、xiの各バージョンがcommitされた状態の一部になり、Tiがxiをinstallするという。

transaction hisotires DBのtxn履歴を txn historyと呼び、それは２つの要素で構成される。 - イベントの半順序 E: - Eはtxn内のイベントの順序を保存する。イベントはread/commit等の操作を表す。 - いくつかの制約を持つ。例えば「txnがxを修正した後にxを読み込んだ場合、xの最終更新版が得られる」など。
- バージョン順序 <<: - commitされたtxnによって作成された各オブジェクトのバージョンの全順序 - バージョンxi, xjがあった時、xiがxjより前にあれば、 xi << xj

数学の半順序とは関係ない。たぶん。

historyに関しては、更にいくつかの制約がある。
例えば、もしwi(xi:m), ..., ri(xj)という履歴があり、間にwi(xi:n)がなかった場合、xjはxi:mでなければならない。 この条件は「もしtxnがオブジェクトxを修正した後にxを読み込んだら、xの最終更新版が得られること」を保証している。 その他の制約は論文を参照してほしい。

因みに、historyのバージョン順序はHのcommitされたイベントの順序とは異なっており、この柔軟性が楽観的なマルチバージョンに対応するために必要ならしい。
事実、マルチバージョンでは、「xjがxiより先にinstallされるが、xi << xj」という状況があり得る。

出典: [1]

predicates txnが述語Pに基づいてread/writeを実行するとき、システムはPのテーブルにある各タプルに対してバージョンを選択する。選択されたバージョンのセットは、この述語ベースの操作のバージョン・セットと呼ばれ、Vset(P)で表現される。

道具の用意2: Conflicts and serialization graphs

まず、txn間のコンフリクトをタイプ別に定義した後、それによってserialization graphを定義する。

まずはコンフリクトの定義。

directory Read-Depends 以下のいずれかの条件を満たすとき、txn Tjがtxn Tiにdirectory read-dependsである。 - directly item-read-depends... Tiがxiの何かのバージョンを install し、Tjがxiを読み込む - directly predicate-read-depends... Tjが rj(P: Vset(P)), xk ∈ Vset(P), i=k or xi << xkを実行し、xi　＞？？？

出典: [1]

directly anti-depends 以下のいずれかの条件を満たすとき、txn Tjがtxn Tiにdirectly anti-dependsである。 - Directly item-anti-depends ... Tiがxiの何かのバージョンを読み取り、Tjがxの(xiより)後のバージョンをinstallする - Directly predicate-anti-depends ... TjがTiによるri(P: Vset(P))をoverwriteしてしまう(マッチの結果を変えてしまう)

read, anti depend共に、述語に関しては同じような扱いをしており、述語のマッチ(結果)が変化する時に依存が発生するとしている。

directly write-depends Tiがxiをinstallし、Tjがxの(xiより)後のバージョンをinstallする場合、txn Tjがtxn Tiにdirectly write-dependsである。

Direct Serialization Grpah(DSG) histroy Hから生じるDSGをDSG(H)とする。 DSGはDAGであり、ノードとエッジの定義は以下。
ノード Ti : commited txn エッジ Ti -> Tj : Ti からTjに存在する何かのdirect depends

出典: [1]

注意: DSGはcommitされたtxnの情報しか含まないため、history Hの全ての情報をエンコードしているわけではない。

DSGの例
出典: [1]

出典: [1]

DSGによる分離レベル

ANSI分離レベルに対するDSGを用いた仕様も、これまでのアプローチと同様に、各分離レベルで回避すべきphenomenaの観点から各分離レベルを定義するが、このphenomenaがDSGの形によって定義されているのが大きな違いだ。
以下、DSGによるphonomenaをG0~G2で定義していく。

G0: Write Cycles DSG(H) が write-dependency edgeによる有向閉路を持つ。

出典: [1]

出典: [1]

G1は以下のG1-a~cで構成される。
G1-a: Aborted Reads
abortされたtxn T1とcommitされたtxn T2を含み、T2がT1によって更新されたオブジェクトを読み出している。

例)

w1(x1:i) ... r2(x1:i) ... (a1, c2が発生)
w1(x1:i) ... r2(P: x1:i, ... ) ... (a1, c2が発生)

DSGはcommitしたtxnの情報しか含まないから、abortが絡むと表現が難しくなるのかな？

G1-b: Intermediate Reads commitされたT2が、T1の最終的な書き込みバージョン以外のバージョンのxを読み出している。 例)

w1(x1:i) ... r2(x1:i) ... w1(x1:j ) ... c2

w1(x1:i) ... r2(P: x1:i, ...) ... w1(x1:j ) ... c2

G1-c: Circular Information Flow DSG(H)がread/write-dependencyによる有向閉路を持つ。

G2: Anti-dependency Cycles
DSG(H)がanti-dependency edgeを一つでも含む有効閉路を持つ。

G2-item: Item Anti-dependency DSG(H)がitem-anti-dependency edgeを一つでも含む有効閉路を持つ。

G2-itemはG1より若干ゆるい。 実際、以下のようなhistoryはG2-itemに該当するがG2には該当しない。

出典: [1]

出典: [1]

ここまで定義してきたphenomenaを用いて分離レベルPL-1~PL-3を定義する。

出典: [1]

これで、実装に依存しない分離レベルの仕様を定義することができた。

出典:
[1] Generalized Isolation Level Definitions. ICDE, 2000.

論文2について

Dynamoについては、素晴らしいまとめがたくさんあるので、そちらを参照してほしい。
まずはDynamoDBの公式で概要を把握してから、下記リンクを当たると良いと思う。

• 論文の日本語訳
• コンセプトから学ぶAmazon DynamoDBシリーズ ... 全体像がわかりやすく解説されている。また、論文の内容というより今のDynamoDBについて話している。
• AmazonのDynamoDB論文を眺めた... 論文2章あたりの話が纏められている。
• Dynamo: Amazon’s Highly Available Key-value Store... 4章の内容が解説されている。

論文３について

この論文は日本語訳が出ているので読むときはをそれを参照するのがおすすめ。
https://www.infoq.com/jp/articles/cap-twelve-years-later-how-the-rules-have-changed/

今更なんだけど、この論文を書いたEric Brewer氏はCAP定理を提案した本人のよう。

CAP定理とは、ざっくりいうと以下のことを示している。
「分散システムは、一貫性, 可用性, (通信の)分断耐性のうち、いずれか2つしか提供できない」

ここで、CAP定理における一貫性と可用性の定義について補足する。

• 一貫性... 線形化可能性という非常に強い一貫性モデル。線形可能性の定義については、このスライドやwikipediaを参照。
• 可用性... 1つ以上のノードに障害が起きてもクライアントに応答を返す

CAP定理の詳しい話はIBMのサイトが分かりやすい。

CAP定理の意味を図でかんたんに説明する。

以下の図のような２つのnodeがネットワークで繋がれた分散システムを考える。
この２つのnodeはネットワークで同期が取れているとする。
また、node1の変更内容が瞬時にnode2にネットワークを伝って反映されるとしよう。
ここで、ユーザがA=1という書き込みをnode1にしたとする。(ユーザ自身はどのnodeに書き込んだかは分からない)
次にユーザがnode2からAの値を読み込むと、A=1が返ってくる。(ここでも、ユーザ自身はどのnodeから読み込んだかは分からない)

ここで、node1とnode2を繋ぐネットワークに障害が発生したとしよう。
この状況でユーザがnode1にA=2という書き込みをしようとした場合、システムの対応として２つ考えられる。
１つ目は、node1に書き込みを許可するパターン。この場合、その後にnode2から読み込んだ場合A=1が返ってくるので、node1とnode2どちらから読み込むかで値が異なる。

これはある意味、可用性を優先し、(node1,2の)一貫性を放棄している。

２つ目は、node1への書き込みを許可しないパターン。この場合も、その後にnode2から読み込んだ場合A=1が返ってくるので、node1とnode2どちらから読み込んでも値は同じ。

これはある意味、可用性を放棄し、(node1,2の)一貫性を優先している。

ざっくり

• 設計者は一貫性と可用性を最適化し、3つの性質すべての釣り合いを取ることができる
• 一方で、CAP定理の"3つに2つという表現は誤解を生み、３属性の関係を過度に単純化してしまう
  • ある性質を満たすかどうかの２値判定は極端
  • ネットワーク分断(分割)はめったに怒らず、分断のない状態ではAもCも失われない
  • CAPは遅延を無視している
  • 同じシステムにおいて、様々な粒度・軸でCとAの選択を行える (サブシステム, 操作, 関係するユーザ, ...)
  • 一貫性を失う場合のコストを把握するのは難しい
• 現在のCAP定理の目的は、特定のアプリに必要な一貫性と可用性を最適化すること
• 分断が派生した場合のために、分断を検知し明示的に対処する仕組みを作る必要がある
  • 分断の検知-> 動作が制限される分割モードへ明示的に移行 -> 分断中に発生した動作不良を保証(下図参照)

引用: 12年後のCAP定理: "法則"はどのように変わったか

本文で出てくるACID, BASEの説明については、RDSとDynamoDBをCAP定理、ACID、BASEを使って整理するが分かりやすい。

また、CAP定理に関する意見として以下の記事はとても勉強になった。
データーベースをCPだのAPだのと分類するのはやめて下さい

WIP【備忘録】DBの論文を読む : 大規模データフローエンジン

そろそろデータベースに関するちゃんとした基礎知識をつけたいという思いがあるので、Readings in Database Systems, 5th Edition を読んでいこうと思う。
URL: http://www.redbook.io/index.html

この本は、DBに関する古典的な論文から、近年の特に重要な論文まで、章ごとに短い解説とともに紹介されている。

今回は Ch5 大規模なデータフローエンジン を読む。

紹介された論文

1. MapReduce: Simplified Data Processing on Large Clusters. OSDI, 2004.

   • 大規模分散処理技術であるMapReduceの考え方と実装

2. DryadLINQ: A System for General-Purpose Distributed Data-Parallel Computing Using a High-Level Language. OSDI, 2008.

   • Dryadという大規模分散処理技術をプログラマが使いやすいように設計されたインターフェース(拡張言語環境)

解説を読んだ

この章の解説では、MapReduceとそれに続く大規模なデータ処理システムは「過去10年間のデータ管理における多くの開発の中で最も破壊的で最も物議を醸しているものの1つ」としたうえで、従来のDWHとの類似点や重要な違い、そしてこれらの傾向について説明している。

MapReduceの出現は少なくとも３つのインパクトを残したらしい。

1. スキーマの柔軟性
   • 従来のDWHと違い、クリーン/ダーティかに関係なく任意に構造化されたデータを処理できる

2. インターフェースの柔軟性

   • SQLやUDF(ユーザー定義関数)

3. アーキテクチャの柔軟性

   • RDBMSに対するよくある批判の一つに「アーキテクチャが緊密に結合されている」というものがあった
   • 対照的に、Hadoopエコシステムはボトムアップ開発の結果としてDWHを一連のモジュールとして効果的に構築できた

要約すると、今日の分散データ管理インフラストラクチャの主要なテーマは「柔軟性と不均一性」らしい。　　 ここら辺、正直あまりイメージついていない。論文読んだらわかるのかな。

ちなみに、MapReduce自体は「短命」だったらしい。考え方だけが残ったということかな？
確かにインターフェースとしてのMapReduceはあまり見ない気がする。

実際、MapReduceは大規模な適用性をもつアーキテクチャではなく、２つの問題があったとのこと。

In effect Map-Reduce suffers from the following two problems:

1. It is inappropriate as a platform on which to build data warehouse products. There is no interface inside any commercial data warehouse product which looks like Map-Reduce, and for good reason. Hence, DBMSs do not want this sort of platform.

2. It is inappropriate as a platform on which to build distributed applications. Not only is the Map-Reduce interface not flexible enough for distributed applications but also a message passing system that uses the file system is way too slow to be interesting.

出典 Red Book, 5th

論文１について

MapReduceについては、ネット上のリソースが豊富にあるので、良さげなリンクをまとめるに留める。

Abstract

TODO: 今度書く

感想とメモ

• MapReduceの講義ノート: Czech Technical University ... MapReduceとHadoopについてわかりやすく纏まっている。
• MapReduce論文つまみ食い ... MapReduceの論文のサマリ。
• MapReduceの基礎... MapReduce周辺の技術の詳解やMapReduceによる実装例が豊富。
• MapReduceの講義スライド

論文2について

Abstract

• DryadLINQは、大規模な分散コンピューティングのための新しいプログラミングモデルを実現するシステムおよび言語拡張セットだ。
  • LINQ +
    • 強力に型付けされた.NETオブジェクトの表現力豊かなデータモデルを採用
    • データセットに対する汎用的な命令/宣言的操作を従来の高級言語内でサポート
  • Dryad
    • DAGで表現された実行計画, 静的/動的最適化
• DryadLINQプログラムは、データセットに対して副作用のない変換を行うLINQ式で構成された逐次プログラムであり、標準的な.NET開発ツールを使用して記述およびデバッグが可能。
• DryadLINQシステムは、プログラムのデータ並列部分を自動的かつ透過的に分散実行計画に変換し、Dryadの実行環境に渡す。
• この論文ではDrydLINQのコンパイラとランタイムの実装を解説した後、いくつかの実験結果を示している。
  • 240台のコンピュータと960枚のディスクで構成されたクラスタで1012byteのデータをソートする汎用プログラムを319秒で実行できた
  • 代表的なアプリケーションについて、ジョブに使うコンピュータの数に対して実行時間をほぼ直線的にスケーリングできた

感想とメモ

この章でDryadLINQが選ばれた理由は優れたインターフェースであるので、そこをメインでメモっていこうと思う。

DryadLINQとは

MS公式でDryadLINQは以下のように説明されている。

DryadLINQは、大規模なPCクラスターで実行される大規模なデータ並列アプリケーションを作成するためのシンプルで強力かつエレガントなプログラミング環境です。 DryadLINQの目標は、大規模なコンピューティングクラスターでの分散コンピューティングをすべてのプログラマーにとって十分にシンプルにすることです。 出典: DryadLINQ

ざっくり言うと、DryadLINQは「Dryad」を「LINQ」を用いて使えるようにした環境だ。
では、「Dryad」「LINQ」とはそれぞれどんなものなのか。

• Dryad ... MS社の提供する大規模分散処理技術。MapReduceに対抗するもの。
• LINQ ... クエリ機能を C# 言語 (および Visual Basic や場合によってその他の .NET 言語) に直接統合する一連の技術。 NINQは統合言語クエリ(Language-Integrated Query)の略。

LINQについては以下の記事が詳しい。
はじめてのLINQ

dryadLINQのインターフェース

では、具体的にはどのようにクエリを記述できるのだろうか。
dryadlinqの論文にある記述例を引用する。

// 例 格納コーパス内の各クエリの最上位の結果を計算する

// SQL-style syntax to join two input sets: 
// scoreTriples and staticRank 
var adjustedScoreTriples = 
    from d in scoreTriples
    join r in staticRank on d.docID equals r.key 
    select new QueryScoreDocIDTriple(d, r); 
var rankedQueries = 
    from s in adjustedScoreTriples 
    group s by s.query into g 
    select TakeTopQueryResults(g); 
    
// Object-oriented syntax for the above join 
var adjustedScoreTriples = 
    scoreTriples.Join(staticRank,
    d => d.docID, r => r.key, 
    (d, r) => new QueryScoreDocIDTriple(d, r)); 
var groupedQueries = 
    adjustedScoreTriples.GroupBy(s => s.query); 
var rankedQueries = 
    groupedQueries.Select( g => TakeTopQueryResults(g));

なんかすごくsparkっぽいな。
MapReduceのプログラミングモデルも手軽に書くことができる。

public static MapReduce(// returns set of Rs 
    source, // set of Ts 
    mapper, // function from T → Ms 
    keySelector, // function from M → K 
    reducer // function from (K,Ms) → Rs 
) { 
    var mapped = source.SelectMany(mapper); 
    var groups = mapped.GroupBy(keySelector); 
    return groups.SelectMany(reducer); 
}

もう少し詳しく仕様を見ていく。
論文では以下のデータ型が紹介されていた。

• IEnumerable<T> ... LINQ collectionの基本型であり、T型のオブジェクトの抽象的なデータセット。iterator interfaceでアクセスできる。
• IQueryable<T> ... IEnumerable<T>の派生型。 LINQ演算子によって構成された(評価されていない)式を表す。
• DryadTable<T> ... IQueryable<T>の派生型。DryadLINQの計算の入出力。schema等のメタデータも含む場合もある。

これらの特徴は以下。

1. 一般に、ユーザはIEnumerable<T>の具体的な型(具象型)を気にする必要がない
2. DryadLINQは全てのLINQ式でIQueryableオブジェクトを構成し、結果が必要になるまで評価を遅延させる。そして結果が必要になった段階でIQueryableのexpression graphを最適化し実行する。
3. DryadTable<T>の派生型は分散ファイルシステムやNTFS ファイルのコレクション、および SQL テーブルのセットなど、基礎となるストレージプロバイダをサポートする。

入出力の例

var input = GetTable("file://in.tbl"); 
var result = MainProgram(input, ...); 
var output = ToDryadTable(result, "file://out.tbl");

その他、DryadLINQは以下の特徴を持つ。
- LINQ式は強く型付けされているものの、糖衣構文によってユーザがそれを気にしないように工夫されている。
- 分散実行するには、DryadLINQの式の中で呼び出されるすべての関数が副作用のないものでなければならない。 - 再帰や反復を含むアルゴリズムの記述がしやすい。(これは参考リンク先にあるk-meansのアルゴリズム実装例で確認できる)

その他、DryadLINQでk-meansやDT等のアルゴリズムを実装する方法については以下のスライドに記載がある。 https://slideplayer.com/slide/6660936/

インターフェースに関してはこれでおしまいなので、残りは興味がある人だけ...

DryadLINQの仕組み

アーキテクチャとフロー

まずは、Dryadのアーキテクチャについて確認しておこう。

出典: [1]

Dryadのジョブはjob managerによって一元的に管理される。 具体的には以下のようなタスクに対して責任を負う。

1. データフローグラフ(DAG)の初期化
2. クラスタのプロセスをスケジューリング
3. フォールトレランスの提供(プロセスの再実行など)
4. jobグラフの動的な変形

計算をDAGとして表現しているのはMapReduceとの大きな違いの一つか。
MapReduceより表現力が高そう。

次に、全体のフローを確認する。

出典: [1]

はええ。。

コンパイラに関するあれこれ

フローの(3)Compileに関していくつかメモしておく。
DryadLINQはLINQ式を受け取ると、まずはそれを実行計画のグラフ(EPG)に変換する。
ここで、EPGはノードが演算子であり、エッジはその入出力を表す。

RryadLINQは「静的最適化」と「動的最適化」の両方を行う。
まず、静的最適化の殆どはディスクとネットワークI/Oを削減することに重点を置いているらしい。 最適化の例としては以下。 - パイプライン化 ... 1つのプロセスで複数の演算子を実行する。 - 冗長性の排除 ... 不要なハッシュまたは範囲分割を削除する。 - Eager Aggregation ... データセットの再パーティショニングはコストがかかるので、可能な限りダウンストリームの集約をパーティション化演算子の前に移動させる。
- I/Oの削減 ... 可能な場合、一時データをファイルに永続化する代わりに、DryadのTCPパイプとメモリ内FIFOチャネルを使用する。

次に動的最適化だが、これは実行中のジョブから情報を取得し、グラフを動的に変換することを指す。
具体的な話は論文参照。

最適化の図を最後に載せる。最初に静的最適化された後、動的最適化が行われている。

出典: [1]

sparkも実行計画がDAGで表現されていた気がするし、やっぱりsparkと似てるな...

その他情報源
興味が湧いたらちゃんと見る。
- https://www.microsoft.com/en-us/research/project/dryadlinq/ - https://pdos.csail.mit.edu/archive/6.824-2010/notes/l05.txt - https://slidetodoc.com/dryad-linq-for-scientific-analyses-msr-internship-final/ - https://www.slideserve.com/arnon/dryad-and-dryadlinq-powerpoint-ppt-presentation - https://courses.cs.washington.edu/courses/csep552/13sp/lectures/8/dryad.pdf - https://sookocheff.com/post/databases/dryadlinq/ - https://www.classes.cs.uchicago.edu/archive/2021/spring/33100-1/notes/dryadlinq.pdf - https://geeks-world.imtqy.com/articles/J182688/index.html

出典: [1] DryadLINQ: A System for General-Purpose Distributed Data-Parallel Computing Using a High-Level Language

WIP【備忘録】DBの論文を読む : 新しいDBMSアーキテクチャ

そろそろデータベースに関するちゃんとした基礎知識をつけたいという思いがあるので、Readings in Database Systems, 5th Edition を読んでいこうと思う。
URL: http://www.redbook.io/index.html

この本は、DB に関する古典的な論文から、近年の特に重要な論文まで、章ごとに短い解説とともに紹介されている。

今回は Ch4 新しいDBMSアーキテクチャ を読む。

紹介された論文

1. C-store: A Column-oriented DBMS. SIGMOD, (2005)

   • 列ストアのDBであるC-storeに関する論文

2. Hekaton: SQL Server's Memory-optimized OLTP (2013)

   • インメモリOLTPであるHekatonに関する論文

3. OLTP Through the Looking Glass, and What We Found There. SIGMOD, 2008 (2008)

   • OLTP向けDBの標準的な機能にどれだけ処理時間が食われているかを調査した論文

解説を読んだ

ここ20年ぐらいでRDBMS市場は大きく変わったらしい。
特に以下の４つの大きな変化があった。

1. DWH市場では列ストアの優位性が高まる
   • よく使われるスタースキーマ(或いはスノーフレークスキーマ)は一般に非常に大きいことや、特定列のみを取得する用途が多い
2. メインメモリの価格の低下
   • 確かに、RAMの価格の低下は個人レベルでも感じていた
3. NoSQLの台頭
   • 「すぐに使えること」「半構造化データのサポート」を特性として持つ
4. Hadoop・HDFS・Sparkの出現
   • 詳しくは６章を参照とのこと
   • Sparkは仕事でも使っているから個人的に馴染み深い

こうしてみると、1,3,4は私が本格的にデータ分析やCSを学び始めた頃には当然のようにあったので、そんなに新しい技術という感じはしていなかったが、最近の変化だったのかぁという感想。
この章で紹介されている論文はわからない単語が多くて特に大変だった。。

論文１について

Abstract

この論文では、特に読み取りに最適化されたRDBMSの設計を紹介している。
具体的な特徴としては、

• 行単位ではなく列単位でデータを格納
• クエリ処理中にメインメモリを含むストレージにオブジェクトを格納する際には慎重にコーディングしてパッキング
• 現在のテーブルやインデックスではなく、列指向のプロジェクションのオーバーラップしたコレクションを格納
• 読み取り専用トランザクションの高可用性と snapshot isolation を含む、従来とは異なるトランザクションの実装
• B-tree構造を補完するためのビットマップインデックスの使用

等が挙げられる。

また、論文では、TPC-Hのサブセットにおける予備的な性能データを提示している。

感想とメモ

背景

先に書いたように、時代が進むにつれてDWHでは列指向DBが適しているとされるようになった。
(そもそもOLTP/OLAP/DWHって何？という人はこのサイト等で確認してほしい)

DWHはその使用用途から少なくとも以下の要件を満たすことが求められる。

• 高速な読み込み

  • 逆に、書き込み速度はそこまで重視されない

• 少数の列かつ大量の行に対するクエリに最適化されている

  • 逆に、select *等のクエリは余り使用されない
  • 例えば、スタースキーマで設計されている場合はファクトテールブルの行数は非常に多くなる

これらの観点に関して、行指向DBよりも列指向DBは優れているとされる。
簡単に言うと、行指向DBは行単位でデータを持っているため特定列(属性)の効率的な取得ができないが、列指向DBは列単位でデータを持っているためこの操作が効率良くできるというイメージだ。
この２方式のより詳細な説明は以下のサイトを参考にしてほしい。

• https://docs.treasuredata.com/pages/releaseview.action?pageId=331325
• https://dataschool.com/data-modeling-101/row-vs-column-oriented-databases/
• https://www.cs.ucdavis.edu/~green/courses/ecs165b-s10/Column_Store_Tutorial_VLDB09.pdf

C-storeは列指向DBの実装の一つだ。

C-storeの特徴

C-storeは以下の特徴を持つ。
この内、幾つかの特徴は列指向DB一般に言えることに注意。

• DWHのような読み取りに最適化された用途に焦点を当てているが、書き込み頻度の低い用途にも対応
  • 列ストアでのtxnを可能にするハイブリッドアーキテクチャ (WSとRS)
• 必要な属性(列)だけをメモリに取り込み、必要な分析を行うことができる
• 同じ列の属性は同じデータ型であるため、効率的な保存/検索のために情報をエンコードすることができる
  • 圧縮。byteやwordの境界で整列するのではなく、より密に纏められる
  • 「特定のキーでソートされた列のグループ」(projection)を、物理的に連続した空間に格納する
• シェアードナッシングの分散アーキテクチャに対応
  • シェアードナッシングアーキテクチャについては、Gammaを参照
  • 異なるプロジェクションがシステム内の異なるノードに配置されることも想定
  • 並列クエリの問い合わせの高速化 (holizontal partition)
  • システム内のk個のノードに障害が発生しても、DBへのアクセスとデータの回復/クエリ問い合わせが可能 (k-safeのサポート)
• ロック・2PCを使用しない、高速な読み取り(分散)txn (snapshot isolation)
• 列指向のクエリオプティマイザ
  • late materialization

なお、C-storeに含まれる殆どの技術は既に存在していたが、C-storeはそれを纏め上げたところに注目するべきか。

C-store データモデル

C-storeは論理データモデルは一般的なRDBと同じだが、物理データモデルは一般的な行ストアと大きく異なる。

論理データモデル

C-storeの論理データモデルは一般的なRDBと同じく、主キーや外部キーを持つテーブル形式だ。

出典: C-store: A Column-oriented DBMS

物理データモデル

C-storeの物理データモデルは一般的な行ストアとは大きく異なる。
一般的な行ストアはテーブルを直接実装し、別途indexを追加することで高速なアクセスを実現していた。

一方で、C-storeはprojectionと呼ばれる「特定のキーでソートされた列のグループ」のみを実装する。
projectionは論理テーブルにつなげられており、それ故にその長さは繋げられた論理テーブルの行数と等しくなる。
ただし、projectionは外部キーによる結合先の列も含めることができる。

projectionの例

# PROJECTION_NAME (col1, col2, ... | sorted cols)  
EMP1  (name, age | age)  
EMP1  (name, age | name)  
EMP3  (dept, age, DEPT.floor | DEPT.floor) # DEPT.foorは外部キーにより取得したカラム  
EMP4  (name, salary | salary)  
DEPT1 (dname, floor | floor)  

なお、projectionはhorizontally partition、つまり行方向に分割ができる。
分割はソートキー(列)の値範囲により行われ、分割後のデータをsegmentsと呼び、SIDが付与される。
さらに、各セグメント内の行をrecord/tupleと呼ぶ。

また、projectionの集合は以下の要件を満たす必要がある。

• 任意のクエリに対応するため、projectionを組み合わせることで完全なテーブルを構築できる

各projectionはsegmentsに分割されているため、この要件を満たすには各projectionの各segmentのtuple同士を紐付ける仕組みが必要だ。
そのためにStorage KeysとJoin Indicesを導入する。

Storage Keys
Storage Key(SK)はtupleに対して「同じsegmentの異なる列の値が元々論理テーブルで同じ行だった組で紐づくように」付与される値。

Join Indices
テーブルTを復元できる２つのprojectionの組 {T1, T2} があった時、
「T1のM個のsegmentとT2からN個のsegmentへのjoin index」は論理上Mつのテーブルの集合である。
テーブルの内容は、T1のsegment Sに対して(s: SID in T2, k: SK in segment s)となっている。

下例はEMP1からEMP2へのjoin indexの例だ。(EMP1のSID=1を仮定)

出典: C-store: A Column-oriented DBMS

C-storeの構成

C-storeは読み込みに対する最適化と書込み可能の両立を図るために、以下の３つの要素でFigure1のように構成される。　　
- WS (Writable Store) ... insert/update等の書き込みが可能なアーキテクチャ
- RS (Read Optimized Store) ... 読み込みに最適化されたアーキテクチャ. 大容量の情報が扱える.
- Tuple Mover ... WSのレコード(tuple)をRSへ移動させる役割を担う

出典: C-store: A Column-oriented DBMS

RS

RSは読み込みに最適化された列ストアであり、以下の特徴を持つ。

• tupleのSKはsegment内のrecordの序数であり、それ故保存はされず必要な時に計算される
• join indexesは通常のカラムと同じように保存される
• RSの列は以下の４通りのエンコーディングで圧縮される
  • Type1: 自カラムによるソート, ユニーク値が少ない : run length encoding
    • 右tupleのシーケンスで表現される (v: value, f: vが現れる最初のposition, n: vの出現回数)
    • clusterd B-tree indexが使えるらしい
  • Type2: 他カラムによるソート, ユニーク値が少ない : bitmap encoding
    • 右tupleのシーケンスで表現される (v: value, b: vが現れる場所に1, それ以外に0)
    • bitmapはsparseなので、更にrun length encodeされる
    • offset index(positionを値にマップするB-tree)を使うらしい
  • Type3: 自カラムによるソート, ユニーク数が多い : block-oriented delta encoding
    • 前の値からの差分で表現される ex) (1, 4, 4, 5, 5) -> (1, 3, 0, 1, 0)
    • olock-orientedの意味がわかっていない。。。
    • densepack B-tree at block-levelが使えるらしい
  • Type4: 他カラムによるソート, ユニーク数が多い : エンコードなし
    • この場合、エンコーディングは行わない
    • densepack B-tree at block-levelが使えるらしい

エンコーディングの参考

• https://www.youtube.com/watch?v=bUY2-8GHKsQ
• https://techblog.yahoo.co.jp/entry/20190924753251/
• http://www.clg.niigata-u.ac.jp/~lee/jyugyou/info_system/medsys004_printw.pdf

WS

WSはRSと同じオプティマイザを使うため、RSと同じ列ストア・物理DBMS設計となっている。
しかし、効率的な書き込み(更新)txnを実現するため、storage representationは全く異なるものになっている。

• SKは明示的にsegmentに保存される
• WSはRSと同じようにhorizonzal parititionされる
  • よって、RSのsegmentとWSのsegmentは1:1で対応する
• WSはRSと比べて小さいと想定されるので、データの圧縮は頑張らない
• WSのprojectionは(v: value, SK)の集合で表現される (夫々のペアはSKのB-treeで表現される)
  • ソートキーは(s: sort key value, sk: sが最初に現れるSK)の集合で表現される

TODO: jion indexの話

Tuple Muver

Tuple Muver (TM)はその名の通りWSのtupleをRSへ移動させる。
具体的には、tupleのブロックをWSからRSへ移動し、プロセス内のjoin indexを更新する。

TMは更新が必要なすべてのsegmentについて、RSに新しいセグメントを作成する。
新しいsegmentが作成されると、古いsegmentが置き換えられ、古いsegmentを削除することができる。

TMに関しては以下のpdfがわかりやすい。　　
http://dsg.csail.mit.edu/6.830/lectures/lec7.pdf

トランザクション関連のお話

• 書き込みを含むtxnは2PCを用いる。
• 読み込りtxnはsnaphost isolationを用いる。

snapshot isolation

読み取り(read-only)txnを高速にするため、ロックと2PCを使用しない方式であるsnapshot isolationを使用している。
これにより、読み取りクエリは最近のある時点でデータベースにアクセスし、コミットされていないトランザクションがないことを保証できる。

https://ja.wikipedia.org/wiki/Snapshot_isolation

TODO: ここら辺、もう少し書く

クエリ最適化

C-storeで使用しているオプティマイザは以下の特徴がある
- データの圧縮形式を考慮する
- どのprojectionの組み合わせを使用するかを考えてくれる
- late materialization: 実行計画の後ろの方でデータの解凍をおこなう
- メモリの節約

なお、クエリ最適化の図示は以下のpdfがわかりやすい
http://dsg.csail.mit.edu/6.830/lectures/lec7.pdf

分散コミットやリカバリの話は気が向いたら書く。

関連論文

• https://vldb.org/pvldb/vol5/p1790_andrewlamb_vldb2012.pdf
• https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.141.5843&rep=rep1&type=pdf

参考になりそうなリンク

• https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-830-database-systems-fall-2010/lecture-notes/MIT6_830F10_lec15.pdf
• https://sookocheff.com/post/databases/c-store/
• https://dataschool.com/data-modeling-101/row-vs-column-oriented-databases/
• https://blog.csdn.net/The_Time_Runner/article/details/115356992
• https://www.cs.ucdavis.edu/~green/courses/ecs165b-s10/Column_Store_Tutorial_VLDB09.pdf
• https://slideplayer.com/slide/6948535/
• https://web.eecs.umich.edu/~mozafari/fall2018/eecs584/reviews/summaries/summary11.html
• https://medium.com/@ameya_s/c-store-a-columnar-database-1fe7e84d7247

Proceedings of the 31st VLDB Conference, Trondheim, Norway, 2005

論文2について

Abstract

この論文は、Hekatonと呼ばれるメモリ常駐データとOLTPワークロード用に最適化された新しいデータベースエンジンの解説をしている。
HekatonはMicrosoft社のSQL Serverに統合されているインメモリOLTPであり、独立したシステムではない。
Hekatonは以下のような特徴がある。

• 手軽に利用できる

  • ユーザーがHekatonを利用するには、テーブルメモリの最適化を宣言するだけでよい
  • 通常のSQL Serverのテーブルと同じ方法でT‐SQLを使用してアクセスする
    • クエリはHekatonテーブルと通常のテーブルの両方を参照できる
    • txnは両方のタイプのテーブルのデータを更新できる

• 高いパフォーマンス/最適化/同時実行制御

  • Hekatonテーブルのみを参照するT‐SQLストアドプロシージャは機械語にコンパイルできる
  • ラッチの不要なデータ構造と多版型同時実行​制御(MVCC)を使用している

感想とメモ

背景

Hekatonの話に入る前に、インメモリDB(IMDB)とは何か/何故登場したかというところから勉強する。

1970年代に初めて登場したDBMS(System R)は以下のような環境で設計されていた。
1. シングルコアCPU
2. 小容量のRAM

しかし、時は流れCPUの進化やRAM(メモリ)の低価格化・大容量化が進んでいった。
そのため、上記２点を前提にしない、特に大容量のRAMを活かすようなDBMSの開発が進んだ。それがIMDBだ。

インメモリDBの定義をwikipediaから引用する。

インメモリデータベース（IMDBあるいはメインメモリデータベース、MMDB）はデータストレージを主にメインメモリ上で行うデータベース管理システムである。ディスクストレージ機構によるデータベースシステムと対比される。

出典: wikipedia

メモリが大量にあるならディスク上ではなくメモリ上にデータを乗っけちゃえばいいじゃんという発想だ。

IMDBの特徴としては例えば以下のような項目が挙げられる。

• 勿論ディスクよりメモリのほうがパフォーマンスが高い
• キャッシュを利用したシステムより柔軟な制御が可能であり、データ管理方法の最適化ができるかも
• IMDBは内部最適化アルゴが簡素で、(通常のDBより)相対的にCPU命令数が少ない(らしい)
• HDDを使用することによって発生していた問題が無くなる
  • 例1. データとキャッシュのコピーを同期する必要がない
  • 例2. ディスク上に比べて、データの効率良い圧縮/解凍ができる
  • その他、バッファプール, 並列制御(ロック), ロギング/リカバリ...
• ACIDの内、D(永続性)については別途考えないといけない

そんなわけで、この特徴から見るとIMDBは従来の(OLTP)DBに比べてリスクが高そうなので、OLTPというよりOLAP向けなのかなぁという気がするが、 IMDBの普及に従いOLTP分野へも進出してきた。
その一つの例がSQL ServerのHekatonだ。

「HekatonはMicrosoft社(MS)のSQL Serverに統合されているインメモリOLTP」と冒頭で述べた。
インメモリOLTPとはなんだろうか？ MSの公式サイトから引用する。

インメモリ OLTP は、トランザクション処理のパフォーマンスの最適化、データの取り込み、データの読み込み、および一時的なデータのシナリオに SQL Server と SQL Database で使用できる高度な技術です。 ...(省略)...
インメモリ OLTP は、トランザクション処理のパフォーマンスを向上させる SQL Server テクノロジであることに注意してください。

出典: 概要と使用シナリオ

う、うーん。つまるところ、IMDBの技術を使用したOLTPぐらいの理解で良いか。
インメモリOLTPについての話は、引用先のリンクから参照できる17分の動画も分かりやすかった。

OLTPで使用するんだから、勿論、耐障害性を持つ。　

現在では、データがメモリ内にあるからというだけで、障害が発生したときにデータが失われることを意味しなくなりました。 既定で、すべてのトランザクションは完全に持続可能になりました。つまり、SQL Server の他のテーブルと同じ持続可能性の保証があります。
...(省略)...
トランザクション コミット後のどこかの時点で障害が発生すると、データベースがオンラインに戻ったときに、コミットされたデータを利用できます。 さらに、インメモリ OLTP は、SQL Server の高可用性とディザスター リカバリー機能 (AlwaysOn、バックアップ/復元など) と連携します。

出典: 概要と使用シナリオ

インメモリOLTPが特に有効なのは、「高スループット、低遅延txn」の場合である公式サイトに記載されている。

個々のトランザクションの低遅延を保ちながら、大量のトランザクションに対応します。 一般的なワークロード シナリオとして、金融商品の取引、スポーツくじ、モバイル ゲーム、広告配信などがあります。 また、一般的なパターンとして、読み取りや更新が頻繁な "カタログ" もあります。 たとえば、大きなファイルが複数ある場合、各ファイルは複数のクラスター ノードに分散され、メモリ最適化テーブル内にある各ファイルの各シャードの場所を分類します。

出典: 概要と使用シナリオ

一般のインメモリOLTPの話とHekatonの話が混ざっている気がするが、何となくのイメージは掴めたと思う。

インメモリDBの説明は、このスライドの前半部分も分かりやすかった。

• https://db.in.tum.de/teaching/ss15/moderndbs/chapter8.pdf?lang=de

Hekatonの特徴と構成

まずはHekatonの特徴をまとめる。

• SQL Severに統合
• メモリ上に配置するテーブルを選択することができる
  • クエリ(T-SQL)はディスク上とメモリ上のテーブルの両方を参照可能
  • メモリ上のデーブルのみを参照するT-SQLストアドプロシージャは機械語にコンパイルできる
• 完全なACIDをサポート
• メモリに最適化されたindex (ハッシュ、Bw-tree)
• 高い同時実行性
  • どのスレッドもラッチ/ロックを取得せずにテーブルの任意の行にアクセス可能
    • ラッチのないデータ構造によりスレッド間の物理的な干渉を回避
    • MVCC (多版同時実行制御)によりtxn間の干渉を回避

Hekatonは高いスループットを実現するためにtxn毎の実行命令数の削減とCPI(1命令あたりのサイクル数)を低くする必要があった。 そのため、Hekatonは以下の原則を元に設計された。

• メインメモリのインデックスを最適化
  • 複雑なバッファプール管理を避ける
    • インデックス操作はログに記録しない (耐久性はロギングとチェックポイントによって保証する)
• ラッチとロックの排除
  • ラッチやスピンロックによるスケーラビリティ低下を防ぐ
    • 内部データ構造（アロケータ、インデックス、トランザクションマップ, ...）は完全にロック/ラッチフリー
    • MVCC
• リクエストの機械語へのコンパイル
  • 実行時のパフォーマンスを最大化
    • 実行時のオーバーヘッドを削減するため、コンパイル時に多くの決定を行う(ex データ型)

なお、テーブルのパーティション分割はサポートしていない。

Hekatonは以下のコンポーネントで構成される。

• Hekatonストレージエンジン
  • データ、インデックスの管理, txn, リカバリ、チェックポイントなど
• Hekatonコンパイル
  • T-SQLストアドプロシージャのコンパイル
• Hekatonランタイム
  • SQL Serverのリソースとの統合などもろもろ

Hekatonは、既存のSQL Severの資産を可能な限り生かす様に設計されている(のだと思う)。
これらのコンポーネントは図1の様に配置される。

引用: Hekaton: SQL Server's Memory-optimized OLTP

図に関する詳しい説明は論文参照。

各部

インデックスとレコードの読み取り/更新

メモリ上に作成されたテーブルに対して、Hekatonは２つのindexを提供する。
- hash index ... ロックフリーハッシュテーブルを使用 - ハッシュバケットによる分割
- Bw-treeによる範囲index ... B-treeのロックフリー版

indexについて以下を抑えておく。
- indexには実際のデータへのポインタが格納される。
- １つのテーブルに対して複数のindexを作成でき、レコードには常にindexでアクセスする。

下図はテーブルとindexの例。

引用: Hekaton: SQL Server's Memory-optimized OLTP

BeginとEndが気になると思う。
これらは「値が有効であり、期間が厳密に重複していない場合のトランザクションタイムスタンプの範囲」を表している。ざっくりいうと有効時間。
例えば、Johnに関するレコードは時刻10~20まで(John, London, 100)で、20~Tx75まで(John, Longon, 110)で、最新が(John, London, 130)と解釈できる。

赤文字の100は更新に関する所なんだけど、これは論文を参照してほしい。

読み取りについて
読み取りは、読み取り時点の時刻を指定し、有効時間が読み取り時刻と重複するバージョンのみが表示される。

更新について 更新時の操作については論文参照。
更新は新しいバージョンのレコードを作成することで行われる。 古いバージョンはtxnから見えなくなった際にGCされる。

プログラミングとコンパイル

Hekatonを作る上での目標に、

• アドホッククエリの実行を最適化するのではなく、 compile-once-and-execute-many-timesワークロードの効率的な実行(ざっくり、同じクエリの複数回実行)をサポートする
  • HekatonはOLTP向け
• 既存のSQL Serverアプリとの高い言語互換性もつ

というものがある。
これを達成するため、Hekatonはクエリのコンパイル機能を提供する。
また、HekatonコンパイラはSQL Serverの機能(ex メタデータ, パーサー, 名前解決, ...)を再利用している。

恐らく、私達が触れているDBMSではクエリはインタプリタ方式で実行されるだろう。
しかし、HekatonはHekatonコンパイラによってクエリをコンパイルし機械語に変換することができる。
これは(多分)一般のプログラミング言語でいうJIT(Just In Time)コンパイルだろうか。
コンパイラの出力はCコードであり、Microsoft VC++でDLLにコンパイルされ、実行時にロード・実行される。

引用: Hekaton: SQL Server's Memory-optimized OLTP

詳しい実装は論文を参照。

一応、ストアドプロシージャの説明を記載しておく。

ストアドプロシージャ (stored procedure) は、データベースに対する一連の処理をまとめた手続きにして、関係データベース管理システム (RDBMS) に保存（永続化）したもの。 永続格納モジュール (Persistent Storage Module) とも呼ばれる。ストアドプロシージャの格納先はRDBMSの実装により異なり、RDBMSのデータ辞書や専用の格納スペースが用いられている。

引用: wikipedia

トランザクション/MVCC

Hekatonは楽観的な多版同時実行制御(MVCC)を使用することで、ロックを使わずにtxn管理を行う。

Hekatonのtxn管理について論文には記載されているが、ここではMVCCの定義に関する話をするに止めようと思う。
私のここら辺に関する理解が深まったらもう少しちゃんと書きたい。

MVCCについて、wikipediaには以下のように記載されている。

MultiVersion Concurrency Control (MVCC, マルチバージョン コンカレンシー コントロール) は、データベース管理システムの可用性を向上させる制御技術のひとつ。複数のユーザから同時に処理要求が行われた場合でも同時並行性を失わずに処理し、かつ情報の一貫性を保証する仕組みが提供される。日本では多版型同時実行制御、多重バージョン並行処理制御などと訳される。また単にマルチバージョンとも呼ばれる。

MVCCは、書き込み処理（トランザクション）が行われている最中に他のユーザによる読み取りアクセスがあった場合、書き込みの直前の状態（スナップショット）を処理結果として返す。つまり、書き込み中も読み取りができ、読み取り中でも書き込みができる。

MVCCにおいて可用性を達成するには、最低限、全ての処理が「どの順番で」行われたかを確実に記録する必要がある。そのため、タイムスタンプやトランザクションIDなどを用いて全ての更新処理が管理される。

引用: wikipedia

雑に、「複数の状態(スナップショット, バージョン)を管理することで同時実行制御をする方式」ぐらいでも多分良さそう。

より詳しいMVCCの説明は以下の記事がわかりやすかった。

• https://the-weekly-paper.github.io/jekyll/update/2017/06/25/An-empirical-evaluation-of-in-memory-multi-version-concurrency-control.html
• https://stackoverflow.com/questions/5751271/optimistic-vs-multi-version-concurrency-control-differences/39269085
  • OCCとMVCCの違いに関する説明

とはいえ、ここらへんの話はもう少しちゃんと勉強しないと腑に落ちなさそうな気がしている。。

MEMO:後で読む

• https://www.slideshare.net/hironorimiura/nightmvcc
• https://bellsoft.jp/blog/system/detail_586
• https://blogs.sap.com/2016/03/01/from-the-archives-why-snapshot-isolation-is-so-useful/

ロギング・チェックポイント・リカバリ

Hekatonのロギング、チェックポイント、リカバリコンポーネントの設計 は以下の原則に基づいて行われた。

• シーケンシャルアクセスへの最適化
  • 顧客が高速なランダムアクセスを備えたI/Oデバイスではなくメインメモリにお金を使えるように
• 通常時のtxn処理のオーバーヘッドを最小化
  • 作業はリカバリのときに押し込めたい
• スケールする際のボトルネックの解消
• リカバリ中のI/O, CPUの並列処理を有効にする

Hekatonはメインメモリのテーブルに最適化されているが、障害後にこれらのテーブルを回復できるようにtxnの耐久性を確保する必要がある。

ログについて
通常、txnログの末尾がボトルネックであるため、ログに追加されるログレコードの数を減らすと、スケーラビリティが向上し、効率が大幅に向上する。

Hekatonのログについて纏めておく。

• ログは基本的にコミットされたトランザクションのREDOログで構成される
  • UNDOログは記録されない
  • ログにはtxnによって挿入/削除された全てのバージョンに関する情報が含まれている
• index操作のログは記録されない
  • 全てのindexはリカバリ時に再構築される
• txnのコミット時にのみログレコードを生成する
  • WALは使用しない
• 複数のログレコードを1つの大きなI/Oにグループ化する
• DB毎に同時に生成される複数のログストリームをサポート
  • ログの末尾でのスケーリングのボトルネックを回避
  • シリアル化の順序はtxnの終了時タイムスタンプによってのみ決定

ここら辺はインメモリのおかげでシンプルになっているんだろうか。

チェックポイントについて
チェックポイントはリカバリ時間を短縮するために実装されるが、特にHekatonでは以下の２要件を満たすように設計された。

• 継続的なチェックポイント ... チェックポイント関連のI/Oは、txnが蓄積されるにつれて、段階的かつ継続的に発生する
  • 突然頑張りだしてシステム全体のパフォーマンスが突然落ちるのは避けたい
• ストリーミングI/O ... 可能な限りランダムI/OではなくストリーミングI/O

MEMO: ストリーミングI/Oと調べたんだけど結局なんなのか分からんかった。 シーケンシャルI/Oだと思って良い？

チェックポイントは複数のデータ/デルタファイルとファイルとチェックポイントファイルインベントリで構成される。
夫々の役割を確認しよう。

• データファイル
  • 特定のタイムスタンプ範囲で挿入された(挿入と更新によって生成された)バージョンを含む
  • 開いている間は追記のみ可能で、一度閉じるとそれ以降は読み取り専用となる
• デルタファイル
  • データファイルに含まれているバージョンが後で削除という情報を含む
  • デルタファイルとデータファイルは1:1で対応
  • 対応するデータファイルの存続期間中に追加のみ可能
• チェックポイントファイルインベントリ
  • 完全なチェックポイントを構成するすべ てのデータとデルタファイルへの参照を追跡する

実質的に、チェックポイントは圧縮されたログのように考えられる。
リカバリはデータファイル読み込み->デルタファイルによるフィルタリングという流れで行われる。

チェックポイントの作り方やリカバリの詳しい話は論文を参照。

GC

書き込み方法から明らかなように、メモリ上には古いバージョンのレコードがどんどん増えてくる。
そのため、アクティブなtxnからは見えなくなったバージョンを削除する必要がある。

GCと聞くと一般的にはポインタの到達可能性を元に行われることを想像するが、HekatonのGCは「(アクティブなtxnからの)バージョンの可視性」によって行われる。

Hekaton GCは以下の特徴を持つ。

• ノンブロッキング ... アクティブなtxnの処理を停止することはない
• 協調的 ... txnを実行しているスレッドは、ガベージに遭遇したときにそれを削除できる。よって、スキャンの邪魔になるものは事前に削除できる。
• 処理はインクリメンタル ... GCは簡単に調整でき、過剰なCPUの消費を避けるためにGCを開始/停止できる
• 並列的/スケーラブル ... 複数のスレッドで同期を殆ど行わず動作する

GCの詳しい処理は論文参照。

関連論文

• http://www.vldb.org/pvldb/vol9/p1609-larson.pdf
• https://link.springer.com/content/pdf/10.1007/s00778-021-00663-8.pdf

参考

• https://ja.wikipedia.org/wiki/%E3%82%B9%E3%83%88%E3%82%A2%E3%83%89%E3%83%97%E3%83%AD%E3%82%B7%E3%83%BC%E3%82%B8%E3%83%A3
• https://stackoverflow.com/questions/5751271/optimistic-vs-multi-version-concurrency-control-differences/39269085
• https://ja.wikipedia.org/wiki/MultiVersion_Concurrency_Control
• https://docs.microsoft.com/ja-jp/sql/relational-databases/in-memory-oltp/sql-server-in-memory-oltp-internals-for-sql-server-2016?view=sql-server-ver15
• https://deep.data.blog/2013/07/03/sql-2014-in-memory-oltp-hekaton-training-videos-and-white-papers/
• https://sookocheff.com/post/databases/hekaton/
• https://web.eecs.umich.edu/~mozafari/fall2018/eecs584/reviews/summaries/summary14.html https://www.slideshare.net/InsightTechnology/dbts-osaka-2014-d35-hardware-hiroyuki-komori
• https://yizhang82.dev/hekaton
• https://docs.microsoft.com/ja-jp/sql/relational-databases/in-memory-oltp/in-memory-oltp-in-memory-optimization?view=sql-server-ver15
• https://15721.courses.cs.cmu.edu/spring2020/notes/02-inmemory.pdf
• https://www.youtube.com/watch?v=a70jRWLjQFk&list=PLSE8ODhjZXjasmrEd2_Yi1deeE360zv5O&index=3
• https://www.db-siken.com/kakomon/31_haru/am2_18.html

論文3について

Abstract

OLTP向けDBから標準的な機能であるログ、ロック・ラッチ、バッファマネージャを取り除いた場合、どの程度処理速度が向上するかを調査した論文。

感想とメモ

この論文に関してはかなりよく纏まった記事があったので、纏めることはしない。
バッファマネージャ、こんなに処理時間食うのかという感じだった。

• https://tombo2.hatenablog.com/entry/2017/03/01/161426
• https://15721.courses.cs.cmu.edu/spring2020/notes/02-inmemory.pdf

WIP【備忘録】DBの論文を読む : 誰もが知っておくべきテクニック

そろそろデータベースに関するちゃんとした基礎知識をつけたいという思いがあるので、Readings in Database Systems, 5th Edition を読んでいこうと思う。
URL: http://www.redbook.io/index.html

この本は、DB に関する古典的な論文から、近年の特に重要な論文まで、章ごとに短い解説とともに紹介されている。

今回は Ch3 誰もが知っておくべきテクニック を読む。

紹介された論文

1. Access path selection in a relational database management system. (1979).

   • SQL文から実行計画を作成する際に使用されるコストの計算について記載している

2. Transaction Recovery Method Supporting Fine-Granularity Locking and Partial Rollbacks Using Write-Ahead Logging. (1992).

   • DBのリカバリ(回復)アルゴリズムの１つであるARIESに関する論文

3. Granularity of Locks and Degrees of Consistency in a Shared Data Base. (1975)

   • ロックとトランザクションの分離レベルに関する論文

4. Concurrency Control Performance Modeling: Alternatives and Implications. (1987)

   • aaa

5. Transaction Management in the R* Distributed Database Management System. (1986)

   • aaa

解説を読んだ

この章では、DB設計における特に重要な概念として、以下の項目に関する論文が紹介されている。

1. 実行計画 (クエリの最適化)
2. データベースのリカバリ
3. 同時実行制御
4. 分散システム

論文１について

Abstract

SQL のような高レベルのクエリやデータ操作言語では、リクエストはアクセスパスを参照せずに非プロシージャルに記述されます。本論文では、述語のブール式として目的のデータをユーザが指定した場合に、System R が単純な（単一の関係）クエリと複雑な（結合などの）クエリの両方に対して、どのようにアクセスパスを選択するかについて説明する。System R は、データのリレーショナルモデルに関する研究を行うために開発された実験的なデータベース管理システムです。System R は、IBM San Jose Research Laboratory のメンバーによって設計・構築されました。

出典: Access path selection in a relational database management system(筆者訳)

感想とメモ

この論文ではオプティマイザがどのように実行計画を建てるのか、また実行コストの計算方法を解説していた。
正直読み終わったあとも50%ぐらいの理解しかできていない気がする...。
また今度時間のあるときに挑戦したい。

さて、論文の内容に入る前に、そもそもオプティマイザが何故必要であるかを復習する。
SQL は宣言的な言語なので、ユーザーはタプル(レコード)の物理的配置を知らなくていいし、タプルへの効率的なアクセス方法を指定する必要がない。
では誰がそれを指定するかというとオプティマイザがその役割を担う。

すると、オプティマイザはどうやって最適なアクセス方法を選び出すのかという課題が発生するが、この論文ではその話をする。

まずはオプティマイザがどのタイミング動くかを考えよう。
クエリが入力されたら、まずはパーサーにより文法上(syntax)のチェックが行われた後、SELECT list,FROM listやWHERE tree等のクエリブロックに分解される。
そして、クエリで必要なテーブルやカラムをカタログ上に存在するかを確認し、以下のことを行う。

• カタログから統計量や利用可能なアクセスパスの取得を行う
• クエリブロックの評価順を決定する
• コストを最小にするアクセスパスを選択する
  • アクセスパスはstructual modification of the parse treeで表現される

どうやらオプティマイザはこの段階で機能するらしい。
ここら辺の話は Ch1 でもやったのである程度は想像できる気がするな。
ここでの結果は実行計画と呼ばれ、ASL(Access Specification Language)で記述される。
ただ、GROUP BYとかORDERBYはどのクエリブロックに属すんだろう？

一応、Postgres公式から実行計画の説明を引用する。

実行計画は、問い合わせ文が参照するテーブル（複数の場合もある）をスキャンする方法（単純なシーケンススキャン、インデックススキャンなど）、複数のテーブルを参照する場合に、各テーブルから取り出した行を結合するために使用する結合アルゴリズムを示すもの

引用元: PostgreSQL 9.2.4文書 EXPLAIN

上のタイミングからもわかるように、オプティマイザはカタログから取得した統計量をメインに使用し最適なアクセスパスを選択する。

ところで、実行計画はどのように表現されるのか。
例としてPostgresの公式にある例を引用する。

例      
integer列を1つ持ち、10000行が存在するテーブルに対して、単純な問い合わせを行った場合の問い合わせ計画を表示します。    

EXPLAIN SELECT * FROM foo;    

                       QUERY PLAN    
---------------------------------------------------------    
 Seq Scan on foo  (cost=0.00..155.00 rows=10000 width=4)    
(1 row)    

引用元: [PostgreSQL 9.2.4文書 EXPLAIN](https://www.postgresql.jp/document/9.2/html/sql-explain.html)    

ここで気になるのが、Seq Scanとcost=...だと思う。
それ以外の意味はなんとなくわかりそうだ。
まずは、このScanの説明をする。

ScanはRSSからどのようにタプルを取得するかを表している。

少しだけRSSの復習をしよう。
RSSは物理的なストレージに関してアクセスパスやロックなどの管理を行う。
テーブルはタプルの連続したコレクション(ページ)として保存され、更にページの論理的な単位をセグメントと呼ぶ。
１つのページに複数のリレーションが含まれることはあるが、１つのリレーションが複数のページにまたがることはない。
復習終わり。

では、RSSへのアクセスはどのように行うのか。
メジャーな方法を２つ挙げる。

1. セグメント Scan (Full(Seq) Scan)
   • セグメントのすべてのタプルを調査する
   • 特徴: 全てのページを１回ずつ調べる
2. インデックス Scan
   • キーとタプルIDをマップする何らかの別のデータ構造を用いて、インデックスを調査しキーとマッチしたタプルのみを取得する
   • 特徴: 必要なページのみを調べるが、同じページ内の２つのタプルがインデックス上で離れている場合、同じページに２回アクセスする
   • 補足: タプルがインデックス順でセグメントのページに挿入されている、或いはインデックスに対する物理的な近接関係が保たれているとき、インデックスがクラスター化されている、という。

先の実行計画の例にあったSeq Scanは、「テーブルをセグメントスキャンする」という意味だとわかる。

因みに、この２つのScanは追加でSARGS(search arguments)と呼ばれる述語(predicates)を取る事ができる。
SARGを指定した場合、Scanの際にタプルがそのSARGを満たしている場合のみそれをRSI callerに返す。
このため、RSI callのオーバーヘッドを抑えることができる。
ただ、任意の述語がSARGとして指定できるわけではないらしい。

話を戻そう。
次に気になるのがcost=..だが、これはそのクエリの推定コストを示している。
実行計画は(推定)最小コストのアクセスパスであるが、２つの疑問がある。

Q1. コストの計算ってどうやるの？
Q2. 最小コストのアクセスパスの探索方法は？

Q1から取り組もう。
論文によれば、オプティマイザは以下の計算式でアクセスパスのコストを計算する。

Cost = (I/O cost)     + W * (CPU cost)     
     ≒ (Page Fetches) + W * (RSI Calls)    

W: I/OとCPUコストの相対重み    

この計算式はI/Oコストの近似としてページフェッチを、CPUコストの近似としてRSI Callを用いている。
重みWは事前に決めるっぽいんだけど、どうやって決めるんだろうとは思う。

まずは１テーブルのみが関わるようなクエリのコストを計算する場合を考えよう。
この場合、WHERE treeとFROM listのコストが計算できればよい。
このコスト計算にはカタログから得られる統計量を用いる。

「あれ？SELECT listは？」と思ったそこの君。わたしもそう思った。
ただ、行志向DBならどの列を持ってきてもコストが変なさそうな気もする。

最初はWHERE treeのコストを計算する。
計算のため、以下のような統計量を定義する。

リレーションをTとする。    
- NCARD(T) ... Tの濃度    
- TCARD(T) ... Tのタプルをもつセグメントのページ総数    
- P(T)     ... TCARD(T) / (セグメント内の非空のページ数)。 セグメント内でTのタプルを持つページの割合を表す    

TのインデックスをIとする。    
- ICARD(I) ... Iが持つキーのユニーク数    
- NINDX(I) ... Iのページ数    

これらの統計量から、オプティマイザは述語リストの論理因子夫々に対し選択係数Fを算出する。

WHERE treeのコストはこれらを用いて計算する。

論文には計算例がいくつか載っている。
うーん、この結果例のいくつかは上手く咀嚼できない。今度見直そう。

fig1

次いで、FROM listに関するコスト計算を考える。

QCARD (query cardianlity)     
   ... (FROM listに含まれるTのNCARDの積) * (WHERE treeに含まれる論理因子のFの積)    

RSICARD (number of expected RSI calls)    
   ... (FROM listに含まれるTのNCARDの積) * (SARGの選択因子)    

SARGはRSIを通すタプルをフィルタリングすることを思い出そう。

これでWHERE treeとFROM listに関するコストが計算できるので、アクセスパスのコストが計算できる。
論文に記載されているコスト例を引用する。
(predsは述語を表す)

fig2

これでQ1が片付いた。
次にQ2に取り組もう。
さて、１リレーションの最小コストアクセスパスは利用可能なアクセスパスのコストを評価することで得られるが、クエリにGROUP BYやORDER BYが含まれる場合、最小コストのパスを以下の２つに関して調査する必要がある。

1. interesting orderでタプルを取得するアクセスパス
2. unorderdでタプルを取得するアクセスパス

ここで、interesting orderはGROUP BYやORDER BYで指定された順序を指し、unorderdはそれ以外の順序を指す。

何故２つのパスを調べる必要があるのか。
GROUP BYやORDER BYがある場合、aのコストと比較するべきは(bのコスト + QCARDのタプルをソートするコスト)となるからだからだ。

そのため、コストはタプルの並び順と共に計算されることになる。
例えば、インデックスAの昇順でScanする場合、(コストC, A ascend)の組が計算される。
このように夫々のアクセスパスのコストを計算し、最小コストのパスを探すことで実行計画を作成する事ができる。

ここまでの感想としては、個々の説明は何となくわかるものの、全体の関係や実例があまり理解できなかった。。。
ただ、コストがどんな風に計算できるかのざっくりとしたイメージはつけることができたので、そこは良かったと思う。

せっかくなので、論文内でも紹介されているJoinのコストについてもメモしておく。
まずは以下のように言葉を定義する。

外表 (outer relation) ... joinする２つのテーブル(relation)の内、最初にタプルが取得されるテーブル。    
内表 (inner relation) ... joinする２つのテーブル(relation)の内、次にタプルが取得されるテーブル。    
                         これはouter relationから取得したタプルによって異なる。    

まずはJoinアルゴリズムの復習をしよう。
この論文で紹介されているアルゴリズムはNested Loop JoinとMerge Joinだけだが、Hash Joinも広く使用されていると思うのでこれもついでにまとめておく。
ただ、アルゴリズムの解説自体は外部サイトでわかりやすい説明があったのでそれを引用するに留める。

ネステッド・ループ結合(Nested Loop Join)
nested loop joinは以下のようなアルゴリズムだ。

NESTED LOOPS JOINとは，一方の表から1行ずつ行を取り出し，もう一方の表のそれぞれの行に突き合わせて，結合条件を満たす行を取り出す入れ子型のループ処理の結合方法です。

出典: ノンストップデータベース　HiRDB Version 9 パフォーマンスガイド

アルゴリズムのイメージや性質は以下のサイトがわかりやすい。

https://bertwagner.com/posts/visualizing-nested-loops-joins-and-understanding-their-implications/

マージ結合(Marge Join)
marge joinは以下のようなアルゴリズムだ。

MERGE JOINは，結合列でソートして，結合列の値が小さいものから順に突き合わせるため，効率が悪いです。MERGE JOINの中でも，SORT MERGE JOINは，結合するそれぞれの表から行を取り出す際に，作業表を作成しソートするため，特に処理効率が悪いです。

出典: ノンストップデータベース　HiRDB Version 9 パフォーマンスガイド

アルゴリズムのイメージや性質は以下のサイトがわかりやすい。
https://bertwagner.com/posts/visualizing-merge-join-internals-and-understanding-their-implications/

ハッシュ結合(Hash Join)
hash joinは以下のようなアルゴリズムだ。

外表の結合列を基に作成したハッシュテーブルと，内表の結合列をハッシングした結果を突き合わせて表を結合します。 この結合方式をハッシュジョインといいます。
出典: Hitachi Advanced Data Binder AP開発ガイド

解説はおなじみのここがわかりやすい。
https://bertwagner.com/posts/hash-match-join-internals/

次にコストの話をしたいのだが、先にN組のjoinについて幾つか性質を話す必要がある。

N組のJoinについて
N組のjoinは２組のjoinを繰り返すことで行われる。
繰り返しの順序はN!パターン存在し、N-joinの結果の濃度は変わらないが、N-joinのコストはパターンによって大きく異なる。
例えばA, B, Cのテーブルがあった場合、この３つのJoinは、以下のようなパターンが考えられる。

• AとBのjoinを行い、その結果とCをjoinする
• BとCのjoinを行い、その結果とAをjoinする
• AとCのjoinを行い、その結果とBをjoinする

ここで注意したいのが、最初のjoinは次のjoinより先に完了している必要はないということだ。
例えばAとBのjoinで結合されたタプルを取得して直ぐにCとjoinすることで3-joinの結合タプルを得られる。

また、Nが大きくなると組み合わせは爆発的に増えるが、いくつかの工夫によって高速化できる。
- k+1回目のjoinのコストは最初のk個のjoinの方法にはよらないため、部分集合のコストを計算することを繰り返す
- 論理的に不可能なjoinの順番がある場合、それを弾く
- 例えばT1とT2は列Aで結合し、T2とT3は列Bで結合するとき、(T1とT3のjoin) -> (T2とのjoin)は不可能

これでようやくjoinのコストについて説明できる。
例の如く、いくつか言葉を定義する。

C-outer(path) ... pathによって外表をスキャンするコスト    
C-inner(path) ... 全ての述語を適用し内表をスキャンするコスト     
N             ... (適用可能？)述語を満たす外表のタプルの濃度    

MEMO:
ここでいくつか疑問がある。
1. C-innerのpathの意味とコストへの影響関係
2. applicable predicates(適用可能述語)とは？joinに使用している述語で良い？

Nは以下のように計算できるらしい。

N = (これまでjoinしてきた全表の濃度の積) * (全ての(適用可能)述語の選択因子の積)    

これらのコスト値からjoinアルゴリズムのコストが計算できる。

C-nested-loop-join(path1, path2) = C-outer(path1) + N * C-inner(path2)    

C-merge-join(path1, path2) = C-outer(path1) + N * C-inner(path2)    

上の式からわかるように、２つのjoinアルゴリズムのコスト式は同じだ。
しかし、実用上ではmerge-joinの方が高速である場合があるが、それは時折merge-joinはinner Scanのコストが非常に低くなることがその理由の一つだと記載があった。

ただ、Joinのコストに関する話はもう少し詳しくしてほしかった感がある。
私がきちんと理解するにはもう少しわかりやすい資料を探す必要がありそう。

論文には実際にJoinを含むクエリの探索例やネストされたクエリのコストについて記載がされているので、そちらも参照してほしい。

とはいえ、「じゃあ、結局この３つのJoinアルゴリズムはどう使い分ければいいん？」という問の答えは知りたかったので、下記表にまとめた。
(下表はSQL実践入門(ミック)を参考にした)

	Pros	Cons
inner loop	- 駆動表が小さく、内部表のindexが使用できる場合高速 - メモリとディスクの消費が少ない(OLTPに適す) - 非等値結合でも使える	- 双方の表が大きい場合は不向き - CPUに負荷がかかる傾向 - 内部表のindexが使えない場合は不向きか
(sort) merge	- 表がソートされている場合高速 - 大規模な表同士の結合に適する - 非等値結合でも使える	- 表がソートされていない場合低速 - 入力に多数の重複が含まれている場合、低速になる恐れ(tmpdbが使用される) - メモリ消費が激しく、メモリ不足になると性能が大きく下がる
hash	- 非等値結合では使えない - 大規模な表同士の結合に適する	- メモリ消費が激しく、メモリ不足になると性能が大きく下がる - hashテーブルの構築はブロッキング操作(?) -

実行計画について更に興味がある人やSQLの記述に活かしたい人はSQL実践入門(ミック)を読むのがおすすめ。

https://www.amazon.co.jp/dp/B07JHRL1D3/ref=dp-kindle-redirect?_encoding=UTF8&btkr=1

論文２について

Abstract

本論文では、ARIES ( Algorithm for Recouery and Isolation Exploiting Semantics ) と呼ばれるシンプルで効率的な手法を紹介します。
この手法では、trxの部分的なロールバック、細分化された（例えばレコード）ロック、WAL (Write-ahead logging) を用いたリカバリをサポートします。
ARIESでは、システム障害後の再起動時に、敗者となったtrxのロールバックを実行する前に、「失われたすべての更新をやり直すために履歴を繰り返す」というパラダイムを導入しています。
また、ARIESは、各ページのログシーケンス番号を使用してページの状態とそのページのログに記録された更新を関連付けています。
trxのすべての更新は、ロールバック中に実行されたものも含めてログに記録されます。
ロールバック中に書き込まれたログレコードと前進中に書き込まれたログレコードを適切に連鎖させることにより、再起動中の繰り返しの失敗やネストされたロールバックに直面しても、ロールバック中に制限された量のロギングが保証されます。
ARIESはファジーチェックポイント、選択的な再起動と遅延再起動、ファジーイメージコピー、メディアリカバリー、高コンカレンシーロックモード(e.g. increment / decrement) をサポートしています。これらのロックモードは操作のセマンティクスを利用しており、操作のロギングを行う機能が必要です。
ARIESは、実装可能なバッファ管理ポリシーに柔軟に対応しています。様々な長さのオブジェクトを効率的にサポートします。
更に、再起動時の並列処理、ページ指向のREDO、論理的なUndoを可能にすることで、同時実行性とパフォーマンスを向上させます。
...
出典: ARIES: A Transaction Recovery Method Supporting Fine-Granularity Locking and Partial Rollbacks Using Write-Ahead Logging (筆者訳)

感想とメモ

Ariesの論文はかなり難しい...。
web上のリソースを色々見てようやく上辺の理解ができた気がする。
そんなわけで、Ariesの仕組み自体は私が参考にしたリソースを記録するに止める。

TODO: 続き

論文３について

感想とメモ

ロックとトランザクション(以下、txn)の分離レベルを解説している論文。
ここら辺の話はDBの入門書でも見た気がするけど、ロックの階層の話や、AN​​SI SQL標準以外の分離レベルは初めて知った。
この論文もなかなか歯ごたえがあり、証明部分などは追いきれていないので時間があるときに復習したい。

ロックに関するお話

まずは、そもそも「ロックとはなんだったけ」となったので、復習する。
つまるところ、txnの一貫性を保つために同じオブジェクトに同時にアクセスできるユーザーを制限するための機構だ。

ロック

ロックとは、ユーザーがデータベースのテーブルやレコードにアクセスするのを制限する処理です。複数のユーザーが同じテーブルやレコードに同時にアクセスする可能性がある場合に、ロックをかけます。テーブルやレコードをロックすると、一度に 1 人のユーザーだけがデータに影響する処理を行えるようになります。
ロック制御は、複数のユーザーが、データベースの同じレコードに同時にアクセスしたり変更する場合に特に重要です。複数のユーザーが同時に使えるデータベースは便利ですが、問題が発生することもあります。たとえば、ロックしていない場合、2 人のユーザーが同時に同じレコードを変更しようとすると、正確なデータが取得できなかったり、一方のユーザーが必要とするデータをもう一方のユーザーが削除してしまう可能性があります。しかし、いったん 1 人のユーザーがアクセスしたレコードを、他のユーザーが一時的に変更できないようにロックできるようにしておくと、このような問題は発生しません。ロックすることによって、データベースへの同時アクセスによる問題の発生を最小限に抑えることができます。
出典: ACTIAN ロック レベルと分離レベル

さて、ロックについては大きく考えることが２つある。
観点1. どの粒度でロックをかけるか(DB全体？レコード毎？)
観点2. どのようなロックをかけるか？(他の人は読み込みすらできない？読み込みは許す？)

まずは観点1「ロックの粒度」について検討する。

観点1「ロックの粒度」

ロックを掛ける単位(lockable unit)の例が論文に記載されているので、まずはそれを確認する。

locakble unitの例
db, table, area, file, 個々のrecords, 複数のfield値, field値

左から右にいくほど小さな単位になっている。
ここで、「areaって何？」となったのだが、以下のサイトによると表とindexなどをまとめたものっぽい？
他の要素に関してはwikiのデータ階層に記載がある。

http://itdoc.hitachi.co.jp/manuals/3020/3020645050e/FIGURE/ZU060120.GIF
http://itdoc.hitachi.co.jp/manuals/3020/3020645050e/W4500164.HTM

一部要素を階層で表現すると以下のようになる。

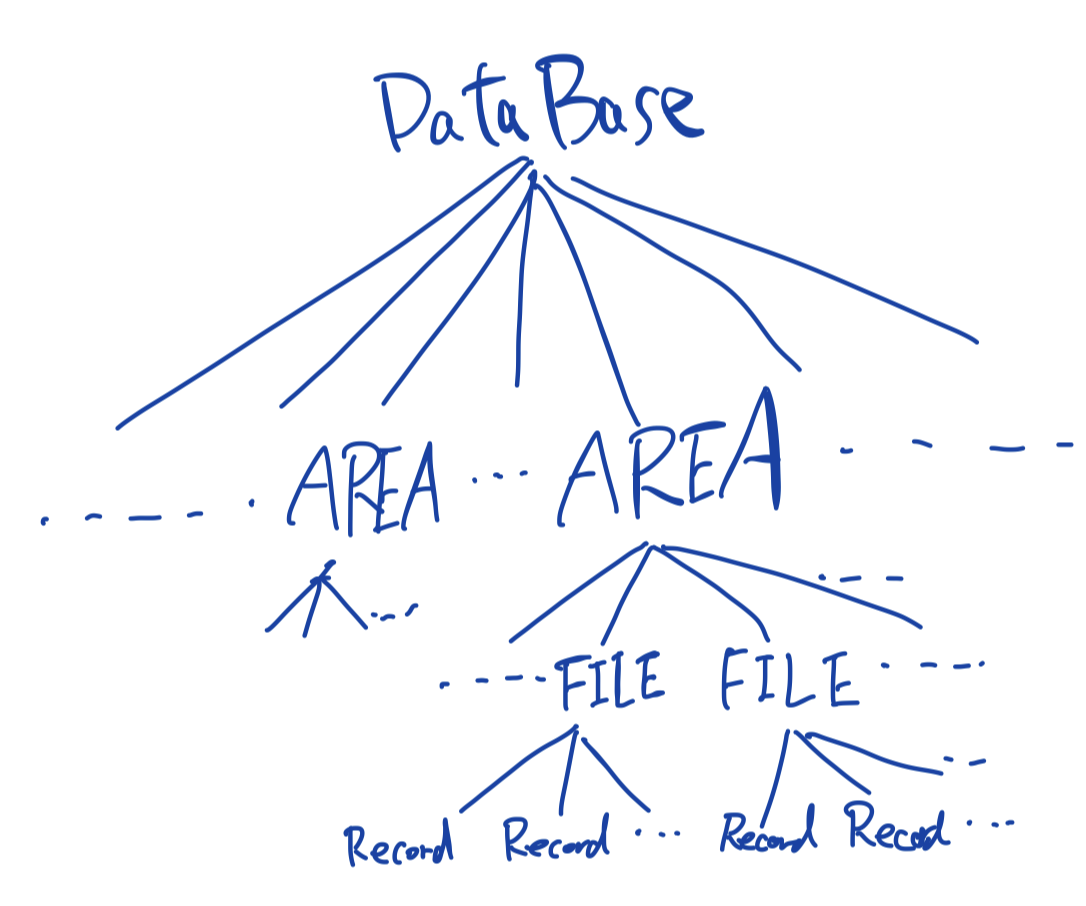
表単位の様な「粗いロック」とレコード単位のような「細かいロック」の選択にはconcurrencyとoverheadに関するトレードオフがある。
細かいロックは並列性が高く、(数レコードしかアクセスしないような)単純なtxnに適している。
反対に、多くのレコードにアクセスするような複雑なtxnに対しては細かいロックはオーバーヘッドが大きくなり、そういった場合は粗いロックが好ましい。

例えば、以下の図のようにFILEに対するロック(黄色)を掛けると、その下にあるRecordsのロック(緑)を纏めて得られる。

【 fig 1 】

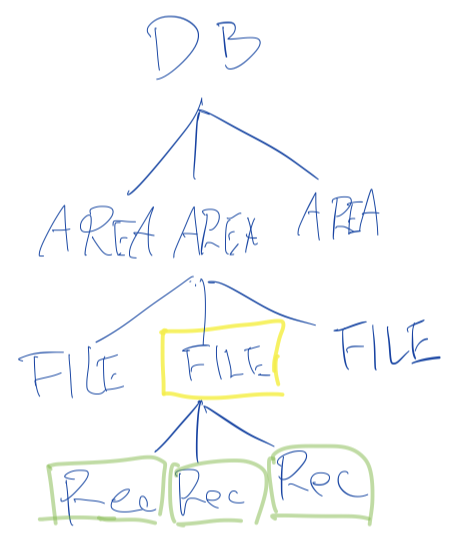
次に、観点2「ロックの種類(モード)」について考える。

観点2「ロックの種類(モード)」
ロックの種類を複数考えることで、一貫性を保ちつつ並列性を高めることができる。
直感的に考えても、「２人が同時に同じレコードを読み込む」ことはOkだが、「誰かが書き込み中のレコードに他の人が読み込みを行う」のはNGだとわかるだろう。

まずはシンプルな２つのロックを考える。

• X (eXclusive) ... 資源を占有する。この間、他者は書き込みも読み込みもできない。レコードの書き込み時などに利用する。
• S (Share）... 資源を共有する。この間、他者は書き込みができない。レコードの読み込み時などに利用する。

例えばAさんがある資源(ノード)のXロックを取得している場合、Bさんはその資源にXロックもSロックも取得できない。
Aさんが取得しているロックがSである場合は、BさんはSロックが取得できる。

なお、fig1のようにFILEに専有ロックが掛かった場合、その下のRecordsにも専有ロックが掛かることに注意。

ロックはこの２種類だけで十分だろうか？
fig1のようにFILEに専有ロックがかかっている場合、そのひとつ上のAREAに専有ロックは取得できないはず(これができてしまうと、その下のFILEに専有ロックが掛かる)だが、今はそれをうまく表現できていない。

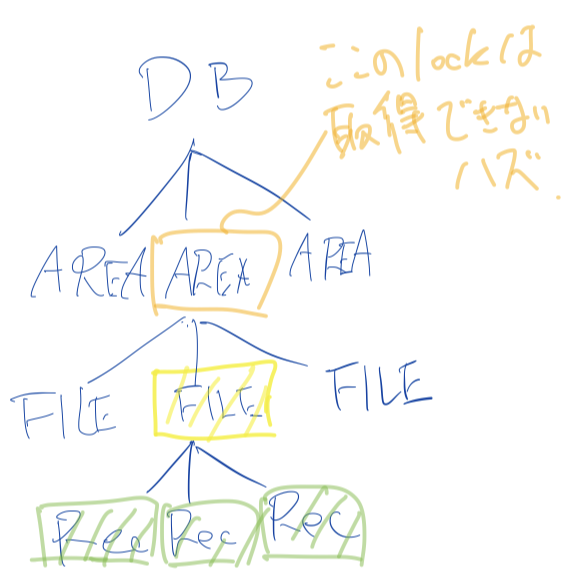
よって、これを解決するため、更にI(intention mode)を考える。
intention modeは「ロックが下位ノード(より細かい粒度)で行われている」ことを示すタグのような役割を果たす。
あるノードのS,Xロックを取得する前にその上位ノードのIロックを取得するようにすることで、全体の整合性を保つ。

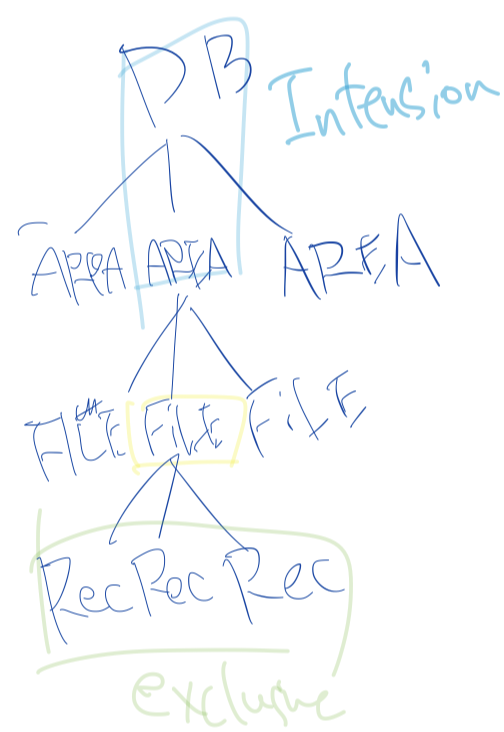
intention modeは以下の３種類を考える。

• IS (Intention Share) ... 資源を意図共有する。 下位ノードのS, ISロックを得られる。
• IX (Intension eXclusive) ... 資源を意図専有する。下位ノードのX, S, SIX, IX, ISロックを得られる。
• SIX (Share and Intension eXclusive) ... 資源を共有・意図専有する。全ての下位ノードのSロックを暗黙的に取得し、明示的に下位ノードのX, SIX, IXロックを得られる。

ISは下位ノードのSロックを取得するために、IXは下位ノードのXロックを得るために用いる。

SIXはかなり曲者だが、「あるFILEのフルスキャンと一部レコードの更新」を考えてみよう。
SIXが無い場合は
(a)FILEのXを取得
(b)FILEのIXとその下位のRecord一つ一つのSorXを取得
のどちらかになるが、(a)は並列性が低く、(b)はロックのオーバーヘッドが高い。
このような用例は多いので、SIXが存在する。

これまで考えてきたロックの両立関係は以下のようになっている。
(NLはNo Lockを表す)

出典: Granularity of Locks and Degrees of Consistency in a Shared Data Base. (1975)

SIXがSの両立とIXの両立の積集合になっている。

また、論文にはロックの半順序関係が記載されている。

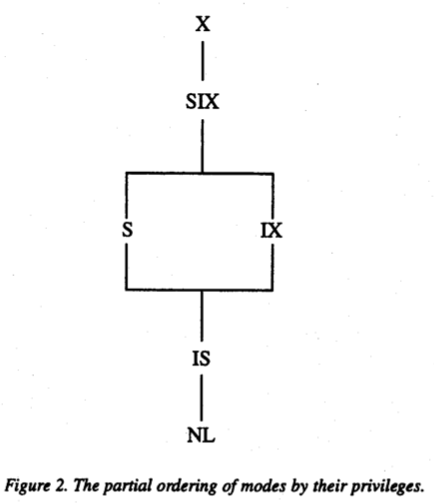
出典: Granularity of Locks and Degrees of Consistency in a Shared Data Base. (1975)

ロックのプロトコル

ロックはroot(最上位)からleaf(最下位)へ要求し、leafからrootへ開放するように使用する。
具体的には以下のルールに従う。

1. あるノードのS,ISロックを要求する前に、その上位全てのノードのIXorISロックを取得する必要がある
2. あるノードのX,SIX,IXロックを取得する前に、その上位全てのノードのSIXorIXロックを取得する必要がある
3. ロックはleafからrootへ開放していく

ロックの例
最後にロックの例を見ていく。

(a) recordRを読み込みたい
1. Rを含むdatabaseのISロックを取得
2. Rを含むareaのISロックを取得
3. Rを含むfileFのISロックを取得
4. RのSロックを取得

(b) fileFの読み込みと書き込みを行いたい
1. Fを含むdatabaseのIXロックを取得
2. Fを含むareaのIXロックを取得
3. fileFのXロックを取得

(c) fileFのフルスキャンとレコードに対して幾つかの更新を行いたい
1. Fを含むdatabaseのIXロックを取得
2. Fを含むareaのIXロックを取得
3. fileFのSIXロックを取得

(a)と(b)は両立できないが、(a)と(c)は両立できることに注意しよう。

この論文には他にも
- データ階層をDAGに一般化した場合のロック
- その他、ロックの正当性の説明
を含む様々な話題が記載されている。

その他参考にした記事
- https://qiita.com/s0t00524/items/56c9d95637d1d356a291
- https://qiita.com/zesu/items/089e1c88259d2b81e41c

txnの分離レベルに関するお話

分離レベルのお話をする前に、まずはtxnについて復習する。

DBはデータに関する言明(assertion)を持つが、それを全て満たしている場合に一貫しているといえる。
しかし、DBを現在の状態から新しい(整合性のある)状態に変更するために、一時的に不整合になる必要がある場合がある。(例えば銀行の送金等)
txnとは、この様な一連の処理を纏めた「一貫性を保つ処理の単位」といえる。

txnについて復習したところで、分離レベルの定義を確認しよう。

トランザクション分離レベル （トランザクションぶんりレベル）または 分離レベル (英: Isolation) とは、データベース管理システム上での一括処理（トランザクション）が複数同時に行われた場合に、どれほどの一貫性、正確性で実行するかを4段階で定義したものである。隔離レベル 、 独立性レベルとも呼ばれる。トランザクションを定義づけるACID特性のうち,I(Isolation; 分離性, 独立性)に関する概念である。

出典: wikipedia トランザクション分離レベル

分離レベルの話はDBの入門書でも書かれていることが多いと思うので、知っている人も多いと思う。
恐らく以下のような定義だろう。(私が知っていたのも以下の定義だ。)

ANSI/ISO SQL標準で定められている分離レベルは、下記の4種類で定義されている。

SERIALIZABLE（直列化可能）
複数の並行に動作するトランザクションそれぞれの結果が、いかなる場合でも、それらのトランザクションを時間的重なりなく逐次実行した場合と同じ結果となる。このような性質を直列化可能性（Serializability）と呼ぶ.SERIALIZABLEは最も強い分離レベルであり、最も安全にデータを操作できるが、相対的に性能は低い。ただし同じ結果とされる逐次実行の順はトランザクション処理のレベルでは保証されない。

REPEATABLE READ（読み取り対象のデータを常に読み取る）
ひとつのトランザクションが実行中の間、読み取り対象のデータが途中で他のトランザクションによって変更される心配はない。同じトランザクション中では同じデータは何度読み取りしても毎回同じ値を読むことができる。
ただし ファントム・リード(Phantom Read) と呼ばれる現象が発生する可能性がある。ファントム・リードでは、並行して動作する他のトランザクションが追加したり削除したデータが途中で見えてしまうため、処理の結果が変わってしまう。

READ COMMITTED（確定した最新データを常に読み取る）
他のトランザクションによる更新については、常にコミット済みのデータのみを読み取る。 MVCC はREAD COMMITTEDを実現する実装の一つである。
ファントム・リード に加え、非再現リード(Non-Repeatable Read)と呼ばれる、同じトランザクション中でも同じデータを読み込むたびに値が変わってしまう現象が発生する可能性がある。

READ UNCOMMITTED（確定していないデータまで読み取る）
他の処理によって行われている、書きかけのデータまで読み取る。
PHANTOM 、 NON-REPEATABLE READ 、さらに ダーティ・リード(Dirty Read) と呼ばれる現象（不完全なデータや、計算途中のデータを読み取ってしまう動作）が発生する。トランザクションの並行動作によってデータを破壊する可能性は高いが、その分性能は高い。

出典: wikipedia トランザクション分離レベル

この論文では分離レベルを次数(degree)0~3までを定義しており、ANSI SQL標準の分離レベルとの対応は以下のようになっている。

• 次数1 - READ UNCOMMITTED
• 次数2 - READ COMMITTED
• 次数3 - REPEATABLE READ
• 次数0, SERIALIZABLEは対応なし

各次数の分離レベルのサマリが以下のように記載されている。

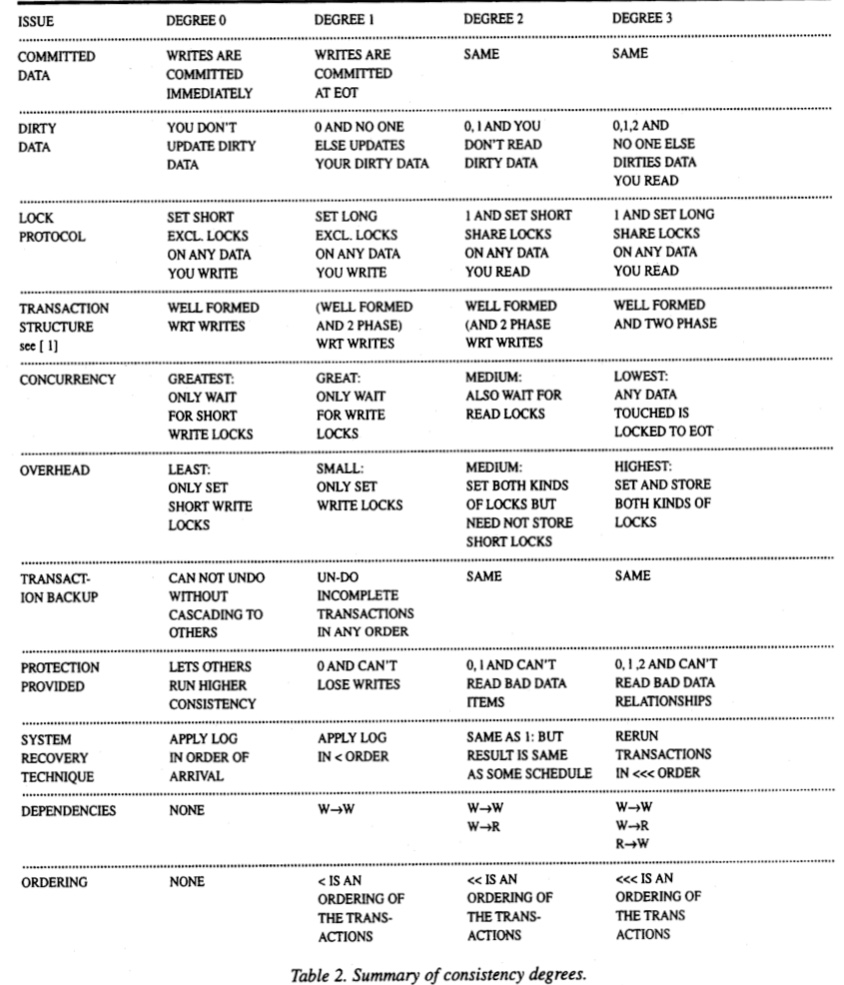
TODO: 語彙に関する補足を記載

その他参考にした記事
- https://blog.acolyer.org/2016/01/06/degree-of-consistency/
- https://qiita.com/song_ss/items/38e514b05e9dabae3bdb

論文４について

論文５について

Abstruct

本稿では、R*分散型データベースシステムのトランザクション管理の側面を扱っています。
主に、R*のコミットプロトコルであるPresumed Abort（PA）とPresumed Commit（PC）の説明に重点を置いています。
PAとPCは、よく知られている2P（two-phase）コミットプロトコルの拡張版です。
PAは読み取り専用のトランザクションとマルチサイトの更新トランザクションに最適化されており、PCはその他のマルチサイトの更新トランザクションに最適化されています。
この最適化により、サイト間のメッセージ・トラフィックとログの書き込みが減少し、その結果、応答時間が改善されました。
また、この論文では、R*の分散デッドロックの検出と解決に関するアプローチについても触れています。
出典: Transaction Management in the R* Distributed Database Management System. (1986) (筆者訳)

感想とメモ

この論文では主に、分散環境でトランザクションを処理する方法として2PC(2相コミット)に基づくプロトコルを説明している。

2PL(二相ロック)と名前が似ているけど、全然別物であることに注意。

というわけで、これから3つのコミットプロトコルについて見ていく。

1. 2PC (two phase commit) ... 2相コミット
2. PA (presumed abort) ... 推定アボート
3. PC (presumed commit ... 推定コミット

前提知識の復習
ただ、いきなりこれらの話題に入る前に予備知識として「分散DB」と「分散トランザクション」について復習する。

分散DBの定義をwikipediaから引用する。　　

分散データベース（ぶんさんデータベース、英: distributed database）は、1つのデータベース管理システム (DBMS) が複数のCPUに接続されている記憶装置群を制御する形態のデータベースである。物理的には同じ場所の複数台のコンピュータで構成される場合や、コンピュータネットワークで相互接続されたコンピュータ群に分散されている場合などがある。

出典: wikipedia

要は「複数のDBを、まるで１つのDBであるかのように使えるようにしたシステム」ぐらいのイメージでいいんじゃないだろうか。

以前にGammaについて勉強したが、これも分散DBの一種だ。

wikipediaよりゆるーい説明としては、ここのサイトがわかりやすかった。
https://itmanabi.com/2phase-commit/

次は分散トランザクションだ。またまたwikiの引用。

分散トランザクション（ぶんさんトランザクション、英: Distributed transaction）は、コンピュータ分野におけるトランザクション処理の処理形態の1つであり、ネットワーク上の2つ以上のホスト（処理するコンピュータ）が関連する、1まとまりの操作（処理、取引、トランザクション）のことを示す。

出典: wikipedia

「複数のマシンが関わるトランザクション」ぐらいの理解で良さそう。
もう少し知りたい人はここを見よう。
https://wa3.i-3-i.info/word16108.html

そんなわけで、分散トランザクション(以下、分散txn)は複数のDBに対する処理(txn)が一纏めになっているため、分散trxのコミットプロトコルも「各DBに対するtxn全てが作動する(commit)か、そのどれも作動しない(abort)」のどちらかでないといけない。

また、一般にコミットプロトコルの望ましい特性として以下が挙げられている

1. 常にtxnの原子性が保証される
2. 短時間の後にコミット処理の結果を「忘れる」機能
3. ログ書き込みとメッセージトラフィックに関するオーバーヘッドが最小限
4. 障害のない場合に最適化されたパフォーマンス
5. 完全または部分的な読み取り専用txnの効果的な利用
6. 一方的なabortを実行する能力の最大化

1は当然として、2の「忘れる」というのは多分txnを「終わらせる」とざっくり言い換えてもいいんだろうか。
3もそれはそう。
4は「障害がない場合のほうが多いよね」という前提のもとでは言えそう。
5は、読み取りtxnは更新がない分最適化できそうだよねという感じは確かにする。
6はabortを強制できる方が何かあった時安全だよねという理解で良い？

この論文ではこの特性の内、パフォーマンスに関わる部分が重点的に説明されている。

2PC 二相コミット

仕組み
2PCではある1つのノードがコーディネーター(幹事)として指定され、他のすべてのノードは従属ノード(部下)として扱われる。
その上で、txnのコミットを行う際に2PCは以下の２段階で実施される。

1. 準備フェーズ
   • コーディネーターは全ての部下にPREPAREリクエストを送信する。
   • 部下は夫々コミットの準備ができていればyesを、コミットができなければnoを返す。
2. コミットフェーズ
   • コーディネーターは、全ての部下がyesを返した場合、全ての部下にCOMMITリクエストを送信する。そうでない場合、全ての部下にABORTリクエストを送る。
     また、このときのCOMMIT/ABORTの判断をトランザクションログとして保存する(コミットポイント)
   • 部下は夫々COMMIT/ABORTレコードを強制的に書き込んだ後、ACkを返す。

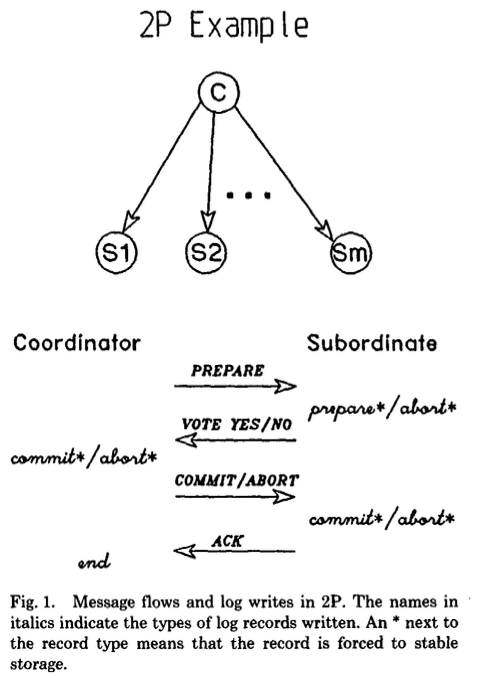
出典: Transaction Management in the R* Distributed Database Management System.

参考: 2PCの更に詳しい説明はデータ指向アプリケーション 9.4.1を見ると良さそう

障害が発生したら
障害が発生した部分がネットワークか部下ノードであれば、以下のような対応になる。
- 準備フェーズ : PREPAREリクエストを送る段階で障害が発生した場合は、障害が発生したトランザクションIDに対するABORTのリクエストを全ての部下に送る。復旧後、障害に関わった部下はコーディネーターに状況を聞く。
- コミットフェーズ : この段階で障害が発生した場合、コーディネーターは成功するまでリトライし続ける。

コーディネーターに障害が発生した場合は、以下のような対応になる。
- PREPAREリクエストを送る前 : 部下のトランザクションは夫々安全に中断される。
- PREPAREリクエストを送った後 : 部下がyes/noを返した場合、それ以降部下は一方的な中断ができず、コーディネータからのリクエストを待つ必要がある。そのため、この時点でコーディネータ(や、ネットワーク)に障害が発生した場合、部下のトランザクションは未確定のまま待ち続けることになる。
- コーディネータの復旧時、トランザクションログを読むことで未確定のトランザクションの状態を確定させる必要がある。
- コミット記録がログに存在しない場合、そのトランザクションは中断される

階層2PC
これまで考えてきた2PCはトランザクションの実行モデルがmultilevel(>2) trees of processが発生する場合は不十分だ、ということで紹介されたのが 階層2PC。

階層2PCではノードはツリーに配置され、各役割は以下のようになっている。
- ルート : コーディネーター
- リーフ : 部下ノード
- 中間ノード : 両方として機能

中間ノードは以下のような動きをする。
- 親からPREPAREリクエストを受信すると、それを下向き(子)に伝播する。
- 子から投票を受け取ると、全ての子がyesを投じた場合はyesを、いずれかの子がnoを投じた場合はnoを上向きに投票/伝搬し、投票がない場合はABORTを送信する。
- 親からABORT/COMMITを受け取った場合、強制書き込みを行った後、親にACkを送信し子にABORT/COMMITを送信する。

PA 推定アボート

PAは、基本は2PCと同じだが、コーディネーターがtxnについて情報がない場合、ABORTだと推定する特徴を持つ。
この変更は以下のようなパフォーマンス上の利点がある。

• コーディネーターがABORTを送信した後、部下からのACKを待たずにtrxを忘れられる。また、部下の名前をABORTレコードに記録する必要もない。
  • 加えて、部下はABORTレコードを強制的に書き込む必要がない
• (部分的な)読み取りtxnの効率化が可能
  • PREPAREを受信し、かつ更新がない場合、READ VOTEを送信し即座にロックを開放しtxnを忘れられる (ログは書き込まれない)
  • コーディネーターはREAD VOTEを送ってきた部下をコミットフェーズから除外できる

以下の状態遷移図はより一般的なものだが、ABORT状態が無いことがわかる。
(IDLEは各プロセスの初期状態と最終状態を示す)

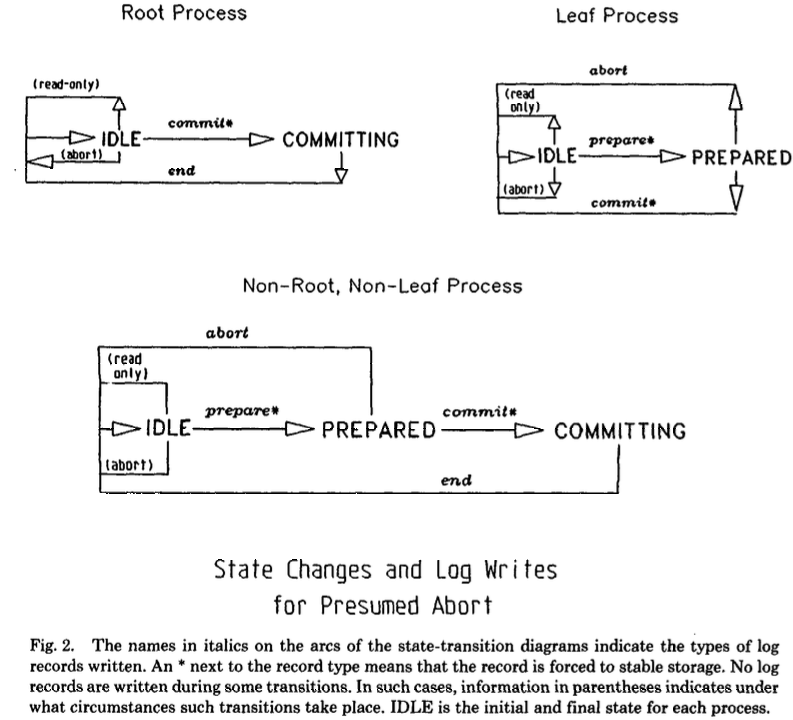
出典: Transaction Management in the R* Distributed Database Management System.

障害が発生した場合の対応は論文か参考サイトを見てほしい。

TODO: 2PCだと読み取りtxnの最適化ができないのか

PC

PCは、基本は2PCと同じだが、コーディネーターがtxnについて情報がない場合、COMMITだと推定する特徴を持つ。
この方式は、「殆どのコミットは成功する」という前提に立っている。
この変更は以下のようなパフォーマンス上の利点がある。

• コーディネーターがCOMMITを送信した後、部下からのACKを待たずにtxnを忘れられる。
  • 加えて、部下はCOMMITレコードを強制的に書き込む必要がない
• (部分的な)読み取りtxnに対してPAと同様の最適化が可能

しかし、以下のような欠点がある。

• コーディネータは部下が準備状態になる前に、部下の名前を安全に記録する必要がある。
  • そうしなければ、準備フェーズの間にコーディネータに障害が起きた場合に不整合が起きてしまう。

このため、PCではコーディネータがPREPAREを送信する前にcollecting record(収集レコード)を強制的に書き込む必要がある。

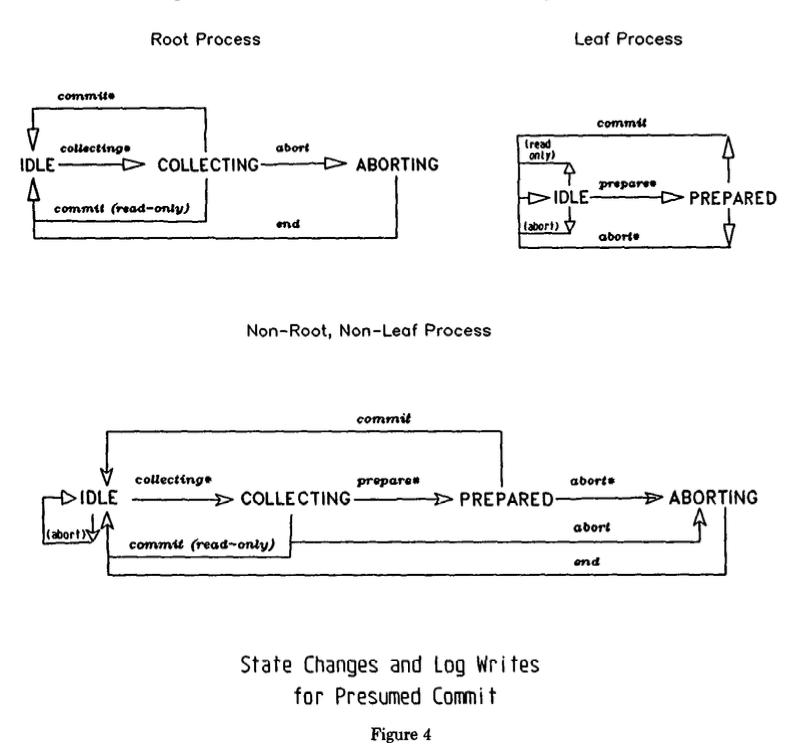
出典: Transaction Management in the R* Distributed Database Management System.

障害が発生した場合の対応は論文か参考サイトを見てほしい。

PCとPAのtxn例が論文に記載されている。

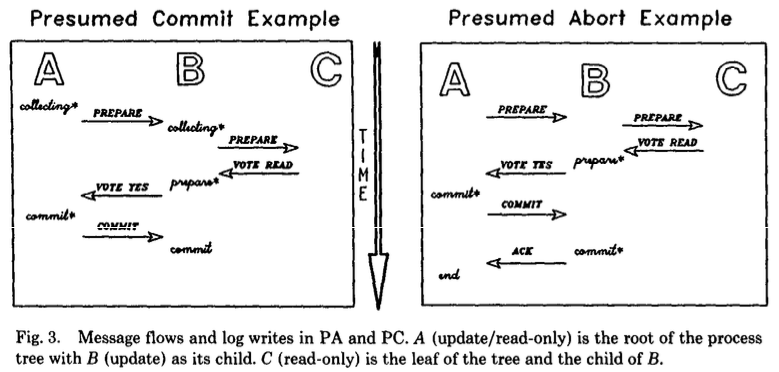
出典: Transaction Management in the R* Distributed Database Management System.

パフォーマンスの比較

この論文によれば以下の通り。

• すべての場合で PAは2PCよりも優れている
• PAとPCのパフォーマンス優位は場合によりけり
  • txnが読み取りのみ ... PAがPCよりも優れている
  • txnが更新を含む ... PCはPAよりメッセージが少ない(ACKの影響)

うーん、なんだか分かったような分かっていないような...微妙な理解度だ。
自分でトランザクションの動きをちゃんと図で書いてみないと理解出来なさそう。

参考
- https://mwhittaker.github.io/prelim_notes/html/transaction-management-in-the-r-distributed-database-management-system.html
- https://blog.acolyer.org/2016/01/11/transaction-management-in-r/
- https://sookocheff.com/post/databases/distributed-transaction-management/
- https://people.eecs.berkeley.edu/~fox/summaries/database/rstar_trans.html
- https://people.eecs.berkeley.edu/~fox/summaries/database/rstar_trans.html

WIP【備忘録】DBの論文を読む : 従来のRDBMSシステム

そろそろデータベースに関するちゃんとした基礎知識をつけたいという思いがあるので、Readings in Database Systems, 5th Edition を読んでいこうと思う。
URL: http://www.redbook.io/index.html

この本は、DB に関する古典的な論文から、近年の特に重要な論文まで、章ごとに短い解説とともに紹介されている。

今回は Ch2 従来のRDBMSシステム を読む。

紹介された論文

1. System R: Relational Approach to Database Management. [System R: DB 管理へのリレーショナルアプローチ] (1976).

   • RDBMS の基礎を構築した論文

2. The design of POSTGRES. [Postgres のデザイン] (1986)

   • ADT の実装に関する論文
3. The Gamma Database Machine Project. [Gamma DB プロジェクト] (1990)
   • シェアードナッシングの普及・分散システム

解説を読んだ

この章では古典的な論文の中で特に重要な論文を時系列で３つ紹介している。
夫々の功績は色々あるが、例えば以下のようなものが挙げられている。

• System R: トランザクションマネージャやオプティマイザ等、RDBMS の基礎
• Postgres: ADT、オープンソースコミュニティのモデル
• Gamma: シェアードナッシングの普及

Postgres は今でも使っているが、この章と前章のデータモデルの論文を読むまで、ADT に関する貢献は知らなかった。何となく使いやすいからとかそんな理由だと思っていた...。

Gamma については名前すら聞いたことがなかった。シェアードナッシングの普及に貢献した論文ならしい。
分散システムの論文を読み慣れていない自分にはいい勉強になったと思う。

ただ、自分の知識不足がいけないんだけど、結局「今はこの実装/考え方はどうなの？」という疑問を終始脇に置きながら読んでしまった感がある。。。

論文 1 について

いつか書く。

論文 2 について

この論文では Postgres の予備設計について解説されている。

Postgres は以下の 6 つの目標を達成することを目指して設計された。

目標 1. 複雑なオブジェクトを使いやすくする
目標 2. ユーザー定義のデータ型や演算子・アクセス方法の提供
目標 3. アクティブなデータベース（アラートやトリガー等のルール処理）と、前向きおよび後向き連鎖を含む推論のための機能を提供
目標 4. クラッシュリカバリのための DBMS コードを簡素化
目標 5. 光ディスクや複数の密結合プロセッサで構成されるワークステーション、およびカスタム設計された VLSI チップを利用できる設計
目標 6. リレーショナルモデルにできるだけ変更を加えないように 1~5 を達成

VLSI って何？と思ったんだけど、weblio によればでっかい IC ぐらいの意味らしい。

1 チップ当たりの半導体素子の集積度が 10 万個を超える集積回路。LSI の集積度をさらに高めたもの。超大規模集積回路。
[補説] 1970 年代以降 1990 年代に至るまで、集積化技術の向上にともない、集積度が 1000〜10 万個程度の LSI、10 万〜1000 万個程度の VLSI、1000 万個を越えた ULSI が登場し、それぞれを区別したが、2000 年代になってからはこのような区別をせず、集積回路全般を LSI または IC と呼称することが多い。
https://www.weblio.jp/content/VLSI

設計目標の議論
目標１、２に関しては Ch1 のデータモデルの論文で詳しく説明されているのを見たほうがまとまっている気がする。
一言で言うなら、「ドメインに合ったデータ型を利用できるようにしたかった」という意図があった。
詳しくは補足を見てほしい。

目標３については、多くのアプリケーションはアラートとトリガーを使用してプログラミングを行うことが多いかららしい。

---

トリガー利用例

例えば、会社の部門テーブルと従業員テーブルがあったとする。部門テーブルのある部門のタプルを削除した時、更新がトリガーされて従業員テーブルからその部門の全ての従業員を削除するようにしたい。

---

目標４については、当時の殆どの DBMS は複雑なクラッシュリカバリコードを含んでいたが、目標２のユーザー定義のアクセス方法を実現するにはクラッシュリカバリのモデルも可能な限り単純で簡単に拡張できる必要がある。

目標５は、単純に可能な限り新しいテクノロジーに対応したかったからというもの。

目標６は、関係モデルが多くの人に利用されるため、できるだけ変更したくないというもの。

---

目標１，２に関する補足

この補足は、Ch1 で紹介されたWhat Goes Around Comes AroundのThe Object-Relational Eraに関する内容を元にしている。

INGRES の初期に、研究チームは次のような単純な GIS(地理情報システム)の問題に悩まされていた。

例えば、交差点の集まりの位置を保存したいとする。

こんな感じ。

Intersections (I-id, long, lat, other-data)  

もしバウンディングボックス(bbox)の中にある全ての交差点を取り出そうとしたら SQL で書くとこうなる。

Select I-id  
    From Intersections  
    Where X0 < long < X1 and Y0 < lat < Y1  

これは INGRES の B 木は１次元のアクセス方法だったので、このシステムではこの２次元の検索を効率よく行えなかった。

範囲内の Parcel(区画)を求めるクエリは更に次元が増える。

Parcel (P-id, Xmin, Xmax, Ymin, Ymax)  

Select P-id  
    From Parcel  
    Where Xmax > X0 and Ymax > Y0 and Xmin < X1 and Ymax < Y1  

この様に、単純な GIS のクエリですら SQL で表現するのは難しく、標準的な B 木で実行すると性能も悪かった。

初期の RDBMS では、整数や浮動小数点・文字列をサポートしていたが、それは元々 IMS のデータ型であったことが主な理由であるし、B 木の採用も、ビジネスデータ処理で一般的な検索を容易にするためだった。

そのため、GIS のような他のドメインでは此等は正しいデータ型ではないし、B 木 が最適でもない。

このように、あるドメインに対応するためには、そのドメインに適したデータ型とアクセス方法が必要だ。
しかし、ドメインにはそれぞれのニーズがあるので夫々で事前に用意するより、自分の特定のニーズに合わせて DBMS をカスタマイズできるようにすべきだと考えた。

そして、その考えを元に目標１，２が掲げられた。

---

論文ではこの後、以下の項目について詳しく書いてある。気分が向いたらまとめようと思う。

• POSTQUEL
• プログラミング言語インターフェース
• システムアーキテクチャ

補足：
目標１，２のための機能については軽くまとめた。
またもやWhat Goes Around Comes Aroundを参考にしている。

目標１，２を達成するため、Postgres の SQL エンジンには以下の汎用拡張機能が追加された。

• ユーザ定義のデータ型
• ユーザ定義の演算子
• ユーザ定義の関数
• ユーザ定義のアクセスメソッド

これらの機能を GIS で利用するには、以下のように定義を追加すれば良い。

• データ型... 地理的な点と地理的な箱
• 演算子(関数)... 「点が矩形にある(!!)」「箱が箱と重なる(##)」

Intersections (I-id, point, other-data)  
Parcel (P-id, P-box)  

Select I-id  
    From Intersections  
    Where point !! “X0, X1, Y0, Y1”  

Select P-id  
    From Parcel  
    Where P-box ## “X0, X1, Y0, Y1”  

以上のようにユーザ定義機能を適切に利用すれば、Quadtrees や R-trees の等の多次元 index と組み合わせると、高性能な GIS DBMS を構築できる。わーい。

また、当時は各ベンダーがストアドプロシージャを導入するためにはエラーメッセージ処理や制御フローを実行するための「独自の（小さな）プログラミング言語」を定義する必要があったが、Postgres UDT と UDF はこの概念を一般化する事で従来のプログラミング言語で書かれたコードを従来の SQL クエリの処理中に呼び出すことができるようにした。らしい。

論文 3 について

Gamma の特徴

Gamma はアーキテクチャを数百のプロセッサに拡張できるように、以下の特徴を持つ。

1. シェアードナッシングを採用している。
2. すべての関係(relations)ば複数のディスク間で水平に分割(シャーディング)される。これにより、関係を並行にスキャンできるようになる。
3. Hybrid Hash-Join を使用し、結合関数や集計関数などの複雑な関係演算子を実装している。
4. データフロー スケジューリング手法を使用して、マルチオペレータクエリを調整する。

ハードウェア構成のセクションは特に気になるところはなかった。

Gamma のソフトウェア・アーキテクチャ

ストレージ構成

Gamma は relations を水平分割している。
これにより、DB は全ての I/O 帯域幅を活用できる。

水平分割と垂直分割の違いは以下の記事がわかりやすい。

• https://towardsdatascience.com/database-terminologies-partitioning-f91683901716

Gamma のクエリ言語は分割方法としてラウンドロビン、ハッシュ、範囲分割を提供している。

この３つの方法は今でも主流っぽい。

また、この論文には「ディスクを持つ全てのノードの全ての relations をデクラスタリングするのは間違っていた」とある。
より優れたアプローチは、負荷分散と全体的な負荷軽減のバランスを取るために、完全なデクラスタリングではなく、可変のデクラスタリングをサポートする仕組みをつくることらしい。
(heat of relations を利用するらしい。関係の疎性とかデータの局所性の話?)

ところでシェーディングとデクラスタリングって同じってことでいいのか？

Gamma プロセス構成
Gamma を形成するプロセスの全体構成は下図。
各ホストのカタログマネージャは各 DB の概念/内部スキーマの中央リポジトリとして機能する。
(その際、各ユーザーがキャッシュしたコピー間の一貫性を保証する必要がある)
また、マルチサイトのクエリはスケジューラプロセスで管理される。
クエリにスケジューラプロセスを割り当てるには、中央のディスパッチプロセスを使用する。
一方で、オプティマイザがシングルサイトのクエリであることを検出したクエリは、スケジューラプロセスを経由せずに、適切なノードに直接送られて実行される。

それ以外の機能については想像がつくと思う。

引用：The Gamma Database Machine Project.　 　

クエリ実行
VAX 版 Gamma のクエリオプティマイザを設計する際、オプティマイザが考慮する可能性のある実行計画のセットは、left-deep-tree のみに制限されていたらしい。これは、right-deep-tree 等をサポートするのに十分なメモリがなかったため。

演算子とプロセスの構造
全ての relational 演算子のアルゴリズムは、単一のプロセッサで実行されるよう記述された。
演算子プロセスへの入力はタプルのストリームであり、出力は分割テーブル(値と出力先プロセスのマッピング)と呼ばれる構造で多重化されたタプルのストリームである。
処理の流れとしては以下のようになる。

1. プロセスの実行を開始
2. 入力ストリームから連続的にタプルを読み込み
3. 各タプルに対して演算を実施
4. 結果として非れたタプルを分割テーブルで指定されたプロセスに転送
5. 出力ストリームを閉じると、各出力先プロセスにend of streamメッセージが送信される

引用：The Gamma Database Machine Project.　

引用：The Gamma Database Machine Project.　

詳しくは論文を参照してほしいが、簡単に例を乗せる。
Figure5 の実行計画をディスクを持つ２つのプロセッサ(P1, P2)とディスクを持たない２つのプロセッサ(P3, P4)で構成される GammaDB で実行する場合の例が Figure6 だ。

引用：The Gamma Database Machine Project.　

引用：The Gamma Database Machine Project.　

Gamma は、クエリの実行に必要な制御メッセージの数がクエリに含まれる演算子の数の 3 倍と各演算子の実行に使用するプロセッサの数にほぼ等しい。
実際、Figure6 の P1,P3 のプロセスに対するスケジューラからの制御メッセージの流れは下図のようになる。

クエリ処理のアルゴリズム
結合演算子以外は一言レベルでの記載にする。

選択演算子
全ての relations は複数のディスク上でシェーディングされているので、選択演算を並列化するにはディスクを持つ関連ノードの上で選択演算子を実行すれば良い。

集約演算子
集約関数は 2 つのステップで計算される。

1. 各プロセッサはパーティションごとに値を計算して結果の一部を算出する。
2. 各プロセッサは「group by」属性のハッシュ化により、部分的な結果を再分配する。

更新演算子（replace、delete、append 等)
標準的な手法で実装される。

結合演算子
Gamma がデフォルトで提供する並列結合アルゴリズムであるHybrid Hash-Joinは、結合される 2 つの関係(テーブル)を各タプルの join 属性にハッシュ関数を適用することにより、バケットと呼ばれる分離したサブセットに分割するというコンセプトに基づいている。

Gamma で実装されるアルゴリズムを理解するために、先ずはそのベースとなる集中型ハイブリッドハッシュ結合アルゴリズムを解説する。

集中型ハイブリッドハッシュ結合アルゴリズム
このアルゴリズムは３つのステップで実行される。
大きな結合が一連のより小さな結合に分割されるのを確認してほしい。

1. ハッシュ関数を使用し、内側の（小さい）関係 R を N 個のバケットに分割する
   • 最初のバケットのタプルはメモリ内のハッシュテーブルを構築するために使用され、残りの N-1 個のバケットは一時ファイルに保存される
   • 小さい方の関係のサイズがバケットの数を決定する
2. ステップ 1 のハッシュ関数を使って関係 S を N 個のバケットに分割する
   • ここでも
   • 最初のパケットは手順１で作成したハッシュテーブルと直ちに probe し結合する
   • 残りの N-1 個は一時ファイルへ
3. アルゴリズムは関係 R からの残りの N-1 バケットを関係 S からのそれぞれのバケットに結合する

Gamma で実装される並列アルゴリズムは、上記の手順について、

• パーティション分割テーブルにより、各論理バケットを夫々ディスクサイトに分割
• ジョイニング分割テーブルにより、タプルをそれぞれのジョイニング・プロセッサ（これらのプロセッサには、必ずしもディスクが接続されている必要はない）にルーティングし、結合フェーズを並列化

等の仕様追加が行われている。

Figure8 は、関係 R が k 個のディスクサイトで N 個のバケットに分割され、最初のバケットが m 個のプロセッサで結合される様子を示している。

引用：The Gamma Database Machine Project.　

トランザクションと障害の管理
Gamma がトランザクションと障害管理のために使用している機構について説明されている。

同時実行制御
Gamma の同時性制御は、2 相ロックに基づいている。
詳しくは論文参照。
2 相ロックの説明自体は以下の記事がわかりやすい。

• https://ja.wikipedia.org/wiki/%E3%83%84%E3%83%BC%E3%83%95%E3%82%A7%E3%83%BC%E3%82%BA%E3%83%AD%E3%83%83%E3%82%AF
• https://ameblo.jp/gokaku-kigan/entry-10407953406.html
• https://qiita.com/s0t00524/items/56c9d95637d1d356a291

リカバリ機構とログマネージャ
オペレータプロセスがレコードを更新する時、DB の状態変化を記録するログレコードが生成される。
これらのログレコードには、ノード番号とローカルのシーケンス番号で構成されるログシーケンス番号（LSN）が関連付けられている。
ログレコードは、クエリプロセッサから 1 つ(或いは複数の)ログマネージャに送信され、ログマネージャは受信したログレコードを結合して 1 つのログストリームを形成する。

詳しくは論文参照。

MEMO: WAL

障害の管理
TODO:書く。